-
Details
-
Hauptkategorie: II. Praxis
-
Kategorie: 9. Astronomische Navigation
9. Astronomische Navigation
I. Astronavigation einfach
(Artikelserie erschienen in: segeln, Juli / Sept / Okt 24)
- Mit dem Sextanten die Sonne schießen
- Nordsternbreite, Mittagposition
- Die Suche nach dem Standort
II. Astronavigation für Einsteiger
1. Überblick
2. Sextant, Sonne schießen, Stellarium
3. Nordsternbreite
4. Mittagsbreite
III. Astronavigation für Fortgeschrittene
5. Umrechnung Zeit in Bogenmaß
6. Mittagslänge, Mittagsposition (Mittagsbesteck)
7. Standortbestimmung aus 2 Messungen
IV. Tagbogen-Verfahren
I. Astronavigation einfach
(Artikelserie erschienen in: segeln, Juli / Sept /Okt 24)
- Mit dem Sextanten die Sonne schießen
- Nordsternbreite, Mittagposition
- Die Suche nach dem Standort
Mit dem Sextanten die Sonne schießen
Überall wird mit Wasser gkocht !
Dies gilt auch für die "Wissenschaft" der Positionsbestimmung mit Hilfe eines Sextanten.
Wer einsteigt, will ohne großen Aufwand auskommen.
Was braucht man?
- Einen Sextanten
Es muss kein hochwertiger Sextant sein. Ein Kunststoff-Sextant tut es auch und sie sind besser als gerne dargestellt.
Der Davis Mark 15 kostet zwischen 280,- und 325,- € (April 2024).
Ein großer Vorteil von Kunststoffsextanten ist - entgegen anderer Behauptungen - dass sie leicht sind.
- Wissen muss man, wie man den Sextanten bedient, um die Sonne zu "schießen".
- Ein künstlicher Horizont zum Üben ist ebenfalls nötig. (Er ersetzt den Horizont auf See.)
Man kann ein Zusatzinstrument für viel Geld erstehen.
Um zu Hause zu üben, eignet sich auch ein Teller mit Wasser als Spiegel für die Sonne.
- Die Uhrzeit zum Messzeitpunkt muss sekundengenau festgehalten werden.
Ein Partner ist dabei hilfreich.
- Die Rechenarbeit kann man einem Computer-Programm überlassen (s. unten).
Der Sextant
… ist ein sehr genaues Winkel-Messinstrument.
(Wikipedia)
Vorneweg eine Warnung:
Der Sextant hat ein Fernrohr (Teleskop), durch das der Navigator auf dem Bild gerade blickt.
Wenn man mit einem Fernrohr ungeschützt in die Sonne schaut, wird das Auge geschädigt.
Daher niemals den Sextanten ohne Filter (Schattengläser) benutzen!
Das Teleskop stellt man scharf wie jedes Fernrohr, durch Drehen am Okular.
Der klassische Trommelsextant
An einem Metallrahmen ist ein beweglicher Zeigerarm angebracht.
Er verbindet den Spiegel oben (Indexspiegel) mit der Gradskala unten.
Jede Veränderung des Indexspiegels verändert die angezeigte Gradzahl am Gradbogen.
Die Feineinstellung auf Minuten und 10tel Minuten geschieht durch Drehen an der Trommel. (Das macht der Navigator gerade im obigen Bild).
Im Sichtfenster der Messeinrichtung werden die ganzen Grade, am Nonius die Minuten und 10tel Minuten abgelesen.
Es ist die gleiche Ablesetechnik wie bei einem Messschieber.
Beispiel:
Die Skala des Sextanten zeigt 59 ° plus etwas :
Auf der Trommel lesen wir die zusätzlichen Minuten ab: 5´ plus etwas :
Dort wo die Teilstriche der Nonius-Skala (rechts) mit den Minuten-Teilstrichen (links) fluchten, ist der 10tel-Wert zu finden: 0,4´ .
Gesamt: 59 ° 05,4 '
Funktionsweise
Wenn man durch das Teleskop schaut, geht der Blick durch den "Horizontspiegel".
Dieser besteht halbseitig aus Normalglas, die andere Hälfte ist verspiegelt. (Das ist im Foto gut zu erkennen.)
Wir setzen die Gradzahl auf 0°. Mit Hilfe einer Sperrklinke kann der Zeigerarm arretiert werden.
(Beim Sextanten im Bild ist es ein drehbarer Knopf unterhalb des Grad-Sichtfeldes.)
Auch die Minutenskala stellen wir auf 0,0´; d. h. der Null-Strich der (drehbaren) Minuten-Skala links muss exakt mit dem Nullstrich
der (festen) Nonius-Skala fluchten.
Der Sextant zeigt nun 0° 0,0´.
Nun richten wir (wie der Navigator oben) den Blick durch das Teleskop auf den Horizont.
Man sieht durch das Fensterglas des Horizontspiegels die eine Hälfte des Horizonts.
Die andere Hälfte wird ergänzt durch die Reflexion der Lichtstrahlen, die vom Horizont kommend vom Indexspiegel oben
auf die Rückseite des Horizontspiegels geworfen und von dort ins Auge des Betrachters geleitet werden.
Ergebnis:
Wir sehen eine durchgehende Horizontlinie, denn der eingespiegelte Horizont setzt den tatsächlich gesehenen Horizont
scheinbar nahtlos fort.
Wenn der Zeigerarm nicht bei 0° stehen würde, sondern z. B. bei 60 °, würde ein Objekt eingespiegelt,
das sich dort (60° über dem Horizont) befindet, z. B. die Sonne.
Dann würden wir links den Horizont und rechts die eingespiegelte Sonne wahrnehmen.
Bevor wir nun die "Höhe" eines Gestirns, den Winkel z. B. der Sonne über dem Horizont, tatsächlich messen,
muss erst überprüft werden, ob der Sextant zehntel-minuten-genau misst oder abweicht.
In diesem Falle müsste man korrigieren.
Diese Korrektur nennt man …
Index-Berichtigung (IB).
Dazu stellen wir die Gradzahl – wie eben - auf exakt 0° 0,0 ´ und betrachten durch das Teleskop den Horizont
oder eine möglichst weit entfernte horizontale Linie, z. B. einen Dachfirst.
Wenn der direkt durch den Horizontspiegel beobachtete Dachfirst mit dem eingespiegelten Dachfirst eine exakte Linie bildet,
ist alles in Ordnung.
In der Regel gibt es aber einen kleinen Versprung. Ursache ist, dass der Indexspiegel nicht exakt ausgerichtet ist.
Diesen Knick müssen wir begradigen.
Das geschieht durch gefühlvolles Drehen an der Mess-Trommel.
Wenn die Dachfirstlinie gerade durchläuft, lesen wir am Nonius den Betrag dieses Fehlers ab (Indexfehler, IF; auch index error, IE).
Er beträgt z. B. 0,2´.
Nun gibt es zwei Möglichkeiten:
- Entweder man korrigiert durch Drehen an den Verstellschrauben des Indexspiegels bis die Horizontlinie bei 0° 0,0´ ohne Versprung
zu sehen ist,
- oder man korrigiert durch Rechnung.
Weil die Verstellschrauben bei zu häufigem Drehen ausleiern, sollte man bei Werten bis 3´ (Minuten!) durch Rechnung korrigieren.
Das geschieht folgendermaßen:
Liegen die 0,2 ´ des Beispiels innerhalb der Plus-Werte der Skala, zeigt der Sextant also 0° 59,8´, misst der Sextant um 0,2´zu wenig.
Bei einer Messung muss deshalb dieser Betrag addiert werden.
Liegen die 0,2´aber auf der anderen Seite der Null-Markierung, ist der gemessene Winkel zu groß,
und der Betrag muss abgezogen werden.
Sonne schießen
Zuerst das prinzipielle Vorgehen:
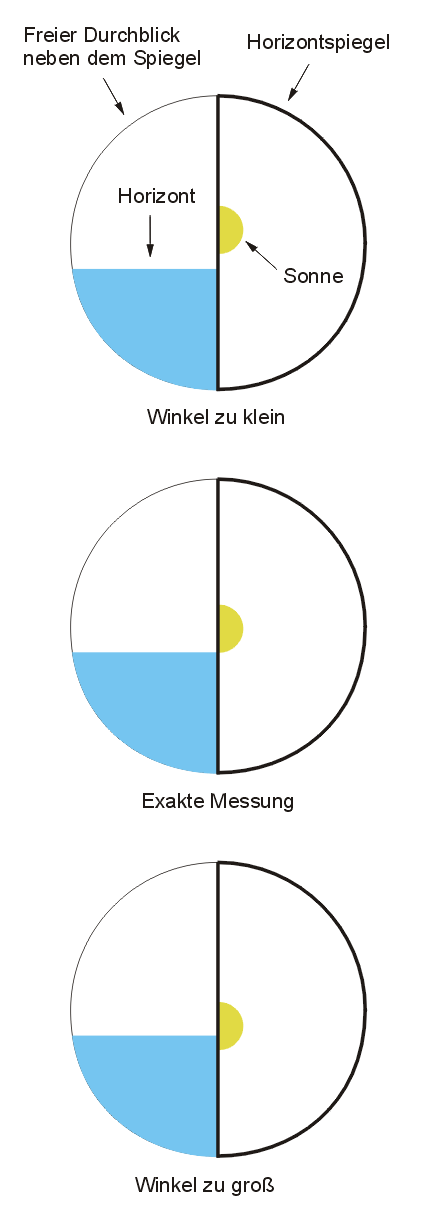
Wir setzen die Sonne mit ihrem Unterrand auf den Horizont, d. h. Sonne und Horizont berühren sich im kleinstmöglichen Punkt.
(Der häufigste Messfehler ist, dass Sonne und Horizont eine kleine Berührungslinie bilden.)
In diesem Moment muss die sekundengenaue Uhrzeit genommen werden.
(Jede unrichtige Sekunde würde die Position um ~ 463 m nach W oder E verfälschen.
Das gilt am Äquator. Erdumfang 40.00 km : 24 h : 60 min : 60 sec = 0.4629 km).
Der am Gradbogen und Nonius ausgelesene Wert ist die "Höhe" der Sonne zum Messzeitpunkt.
Nun zur Praxis:
Der Partner beobachtet seine Handy-Uhr oder die Zeitanzeige am PC.
Als erstes klappen wir sowohl vor den Horizontspiegel als auch vor den Indexspiegel zwei Filter
und suchen die Sonne durch das Fernrohr bei 0°-Stellung am Gradbogen.
Ist die Sonne noch immer zu hell, nehmen wir den dritten Filter dazu.
Dann betrachten wir den Horizont.
Ist das Sichtfeld zu dunkel, verringern wir die Zahl der Schattengläser vor dem Horizontspiegel.
Die Gradzahl ist 0°, wie oben.
Jetzt beginnt der Messvorgang.
Man richtet das Fernrohr auf den Horizont unterhalb der Sonne.
Dann bewegen wir den Zeigerarm langsam von uns weg (kippen also den Indexspiegel nach oben),
so weit, bis die Sonne möglichst knapp über dem Horizont steht.
Nun lassen wir die Feststell-Klemme einrasten.
Durch Drehen am Nonius (wie der Navigator im Bild) holen wir die Sonne weiter auf den Horizont herab,
so, dass sie ihn mit dem Unterrand gerade berührt.
Dabei pendeln wir den Sextanten etwas.
Der tiefste Punkt der entstehenden Pendelkurve ist entscheidend.
Wenn die Sonne den Horizont beim Pendeln "küsst", rufen wir "Jetzt!"; der Partner notiert die Uhrzeit sekundengenau.
Aus Wikipedia:
Das Handling ist nicht ganz einfach ist.
Wenn es nicht klappen will, kann man Folgendes probieren:
Man schätzt den Winkel der Sonne über dem Horizont.
Dazu streckt man einen Arm waagrecht nach vorne, mit dem anderen bildet man einen 45°-Winkel.
Dieser 45°-Winkel dient als Anhaltspunkt für den zu schätzenden Winkel der Sonnenhöhe.
Den geschätzten Wert stellt man im Sextanten ein und richtet den Sextanten auf den Horizont unterhalb der Sonne.
Die eingespiegelte Sonne findet man, wenn man richtig geschätzt hat, etwas unter oder über dem Horizont.
An Land gibt es keinen Horizont. Deshalb muss man mit einem künstlichen Horizont arbeiten.
Ein flacher Teller mit Wasser ersetzt ein teures Zusatzgerät.
Besser ist etwas Speiseöl, weil bei einem Luftzug die Oberfläche nicht so leicht zittert.
- Man muss die Sonne bei offenem Fenster schießen, weil die Fensterscheibe den Strahlengang beeinflussen könnte.
- Der Sextant muss nach oben die Sonne "sehen" können; der Fensterrahmen darf nicht im Wege sein.
- Wenn sich die Sonne im Wasser (oder Öl) spiegelt, gibt es keinen Horizont, auf den man die Sonne setzen könnte.
Man setzt die heruntergeholte Sonne auf den Oberrand der Sonne im Wasser so als wäre diese der Horizont.
- Beim Eingeben in das Astro-Programm von uns (s. unten) wird die Augeshöhe über dem Wasserspiegel (Ah) verlangt.
Bei einem künstlichen Horizont beträgt sie 0 m, wenn man dicht am Teller misst.
Zu diesem Zweck sollte man sich setzen oder den Teller z. B. auf einen Bücherstapel positionieren.
- Bei einem künstlichen Horizont verdoppelt sich der Messwinkel durch die Spiegelung.
Deshalb müssen die Ergebnisse halbiert werden.
(Umgekehrt muss die geschätzte Höhe der Sonne bei Verwendung eines künstlichen Horizontes für eine Voreinstellung
verdoppelt werden.)
- Die Genauigkeit der Uhrzeit von Handy oder PC sollte überprüft werden.
Das kann man am einfachsten mit dem Zeitsignal des Fernsehers.
- Die Uhrzeit ist in UTC umzurechnen.
Umrechnung MEZ in UTC
Früher sprach man von "Greenwicher Zeit" (GMT) , weil der Null-Meridian durch Greenwich verläuft.
Heute heißt sie UTC (Universal Time Coordinated).
In Deutschland gilt nicht UTC sondern Mitteleuropäische Zeit (MEZ).
Die Uhren sind bei uns um 1 h weiter als in Greenwich.
Wenn es in Greenwich 12.00 ist, ist es bei uns bereits 13.00 Uhr.
Um unsere Zeit in UTC auszudrücken, muss also 1 h abgezogen werden.
Als Formel: MEZ – 1 = UTC
Für die Sommerzeit (MESZ) gilt:
MESZ – 2 = UTC
Kostenloser Download
Nun können Sie die Messergebnisse in ein Astro-Programm eingeben.
Dazu stellen wir einen Download kostenlos zur Verfügung bei:
Dort finden Sie weitere Hinweise zur Handhabung des Programms.
Weitere Infos unter:
www.Lampalzer.de > Handbuch für Yachten > II. Praxis > 9. Astronomische Navigation
Ein Praktiker kann nun loslegen.
Ob die gefundene Position identisch ist mit Ihrer tatsächlichen Position, zeigen die Gradangaben bei Google Maps.
Jene, die Lust auf mehr bekommen haben - den astronomischen Hintergrund - vertröste ich auf die nächste Folge Ihrer Segelzeitschrift.
- - - - -
Astronavigation einfach, Folge 2
Nordsternbreite, Mittagposition
Die Segler vor 200 Jahren waren nicht klüger als wir Segler heute.
Ärmel also hochkrempeln und ohne Berührungsängste hinein in die Materie!
Dieses Mal geht es um das Verständnis einfacher, klassischer Verfahren.
Zunächst eine Wiederholung der …
Grundlagen
- Breite, Länge
(Wikipedia)
1 Breitenkreis
2 Meridian (halber Längenkreis)
In der folgenden Skizze wird deutlich, dass sowohl die Breite φ (auch Φ = Phi; engl. Latitude, Lat.)
als auch die Länge λ (= Lambda, engl. Longitude, Long.) Winkel sind, die vom Erdmittelpunkt aus gemessen werden.
(Wikipedia)
Φ ist im griechischen Alphabet der Großbuchstabe, φ der Kleinbuchstabe.
Im astronomischen Zusammenhang bedeuten sie dasselbe.
(Die astronomischen Bezeichnungen sind griechisch, lateinisch, englisch, deutsch - je nach Verfasser und daher verwirrend.)
Der Abstand zwischen zwei Breitenkreisen beträgt 1°.
Bei 40.000 km Erdumfang ist 1° (40.000 : 360 ) 111,11 km
1´ (111,11 : 60) 1,852 km = 1 sm
60 ´ sind 1 °, und damit 1° = 60 sm
Für die Längenkreise (Meridiane) gilt diese Rechnung nur am Äquator. Zu den Polen hin verkürzen sich deren Abstände.
- Höhe, Höhenwinkel (h; Altitute, ALT)
So heißt der mit dem Sextanten gemessene Winkel zwischen Horizont und Gestirn.
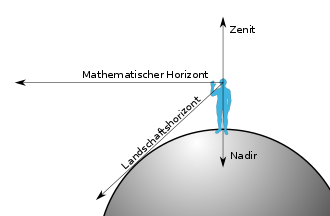
- Zenit (Z)
Der Zenit ist die nach oben verlängerte Lotrichtung eines Standortes.
- Bildpunkt (BP, engl: Geographical Position, GP)
… ist der Punkt, an dem eine gedachte Linie vom Mittelpunkt der Sonne zum Mittelpunkt der Erde die Erdoberfläche durchdringt.
Für einen Beobachter, der auf der Erdoberfläche im Bildpunkt der Sonne steht, befindet sie sich im Zenit.
(Die Definitionen gelten für alle Gestirne. Ich beschränke mich in allen Beiträgen auf die Sonne.)
- Deklination der Sonne (δ = Delta; Dek., engl. Declination, Dec.)
… ist die geographische Breite, auf der ihr Bildpunkt dahinrast.
Die Sonne bewegt sich im Jahresverlauf zwischen
den Wendekreisen N, Wendekreis des Krebses (23,43472°),
und S, Wendekreis des Steinbocks (- 23,43472°)
hin und zurück.
Am Tag der Sommersonnenwende (21. Juni) steht sie am weitesten nördlich, am Tag der Wintersonnenwende (21. Dez.) am weitesten südlich.
Wenn die Sonne den Äquator überquert - zur Zeit der Tag- und Nachtgleiche - ist ihre Deklination 0 °.
(Wikipedia)
Die Deklination der Sonne verändert sich im Verlauf des Jahres alle vier Tage nur um durchschnittlich 1°.
Aber das Tempo der Änderung schwankt: an den Tagen der Sommer- und Wintersonnenwende sind es jeweils 0,1´,
an den Tagen von Tag- und Nachtgleiche (21. 3. und 21. 9.) sind es 23,7´.
Die Deklination der Sonne ist im Nautischen Jahrbuch aufgelistet.
(Auch die Länge, der sog. Greenwicher Stundenwinkel. Darüber später.)
Nautisches Jahrbuch (NJ)
Das Nautische Jahrbuch war das amtliche Handbuch für die astronomische Navigation.
Es enthielt die Ephemeriden (= Positionen) von Sonne, Mond und ausgewählten Sternen für jeden Tag eines Jahres
in einstündigem Abstand. Zwischenwerte konnten interpoliert werden.
Und zusätzlich eine Reihe von Tafelwerken.
2020 wurde das letzte amtliche Nautische Jahrbuch vom Bundesamt für Seeschifffahrt und Hydrographie (BSH) verlegt.
Seit 2023 wird es wieder privat ediert.
Beschickungen
… sind Korrekturwerte bei Sextantmessungen,
- z. B. der Messfehler des Sextanten selbst (Indexerror, IE)
- oder die unterschiedliche Strahlenbrechung des Lichtes (Refraktion) bei verschiedenen Einfallswinkeln an der Erdatmosphäre.
Korrigiert muss auch werden,
- ob der Sonnenunterrand oder - oberrand gemessen wird.
Denn maßgeblich ist der Mittelpunkt der Sonne.
Schließlich spielt auch die
- Augeshöhe (Ah) eine Rolle.
Die Bezugsebene in der Astronavigation ist der Meeresspiegel.
Der Messpunkt , die Augeshöhe, kann in ihrer Höhe erheblich davon abweichen, z. B. h und H in der folgenden Skizze,
wenn dort gemessen würde:
(Wikipedia)
Gesamtbeschickung (GB) heißt die Summe aller Korrekturen, die bei jeder Sextantmessung angebracht werden muss.
Im NJ gibt es hierfür Tabellen; Computerprogramme berücksichtigen die GB automatisch,
lediglich Indexberichtigung (IB) und Ah müssen eingegeben werden.
- Sextantmessungen
 (Wikipedia)
(Wikipedia)
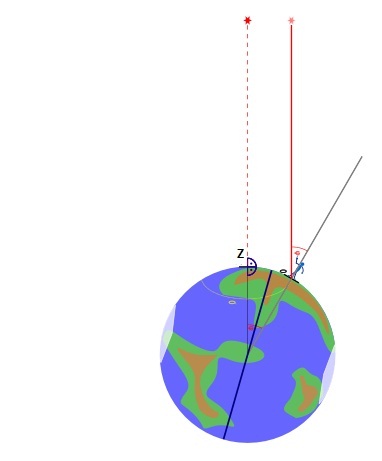
Die Sonne ist so weit entfernt, dass ihre Strahlen quasi parallel in Z und O (dem Standort des Beobachters) auftreffen.
Der Beobachter misst mit dem Sextanten den Winkel zwischen Horizont und z. B. dem Unterrand der Sonne, die Sonnenhöhe (h).
Zenit und Horizont stehen im 90°-Winkel zueinander.
In der Skizze ist nicht der Winkel h sondern der Komplementärwinkel 90° - h rot eingezeichnet.
(Dieser Winkel heißt Zenitdistanz, ZD).
Höhe + Zenitdistanz ergeben immer 90°: h + ZD = 90°
Der Ort, in dem die Sonne im Zenit steht, ihr Bildpunkt, ist mit Z markiert.
Nordsternbreite
Es ist ein relativ einfach zu durchschauendes Verfahren.
Damit kann man auf der Nordhalbkugel mit Hilfe des Polarsterns (Nordstern) die Breite des Beobachterstandortes bestimmen.
Die Höhe des Nordsterns ergibt direkt die Breite des Beobachters.
Wie findet man den Polarstern?
Wenn man die Hinterachse des Großen Wagens (auch: Großer Bär) 5 x verlängert, stößt man auf den Polarstern.
Er ist gleichzeitig der Deichselstern des Kleinen Wagens (Kleiner Bär).
Am nächtlichen Himmel kreisen die Sterne um ihn, er ruht.
(Wikipedia)
Zurück zur Skizze Sextantmessungen:
Nicht die Sonne soll gemessen werden, sondern der Polarstern.
An die Stelle der Sonne (in der Skizze) tritt der Nordstern (Polarstern).
Der Nordstern steht genau über dem Nordpol.
Z wird damit zum Nordpol.
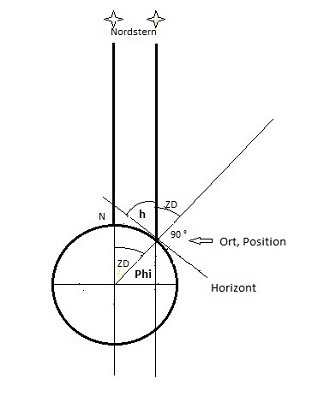
Von der Wikipedia-Skizze nun zu meiner.
Gezeigt wird die Erde, auf ihr die Beobachterposition (Ort, Position). N ist der Nordpol.
Wichtig für das Verständnis ist wiederum, dass die Lichtstrahlen eines Gestirns parallel auf die Erde auftreffen.
Gemessen wird mit dem Sextanten die Nordsternhöhe h.
Die Zenitdistanz ZD errechnet sich aus 90 – h.
Auf der Erdoberfläche ist der Abstand vom Äquator zu den Polen jeweils in 90 Breitenkreise aufgeteilt.
I) Auf welchem Breitengrad man auch den Nordstern misst, immer ergeben
der gemessene Winkel h (Höhe) plus die davon abhängige Zenitdistanz (ZD) 90 Grad.
h + ZD = 90
h = 90 - ZD
II) Der Winkel ZD wiederholt sich am Erdmittelpunkt (Wechselwinkel an Parallelen).
Auch hier liegt ein rechter Winkel vor.
ZD + 𝜑 = 90
𝜑 = 90 - ZD
III) I und II lassen sich also gleichsetzen:
h = 𝜑
In Worten:
Der gemessene Winkel h (zum Polarstern) entspricht dem Breitengrad 𝜑 des Beobachters.
Es gibt zwei Probleme:
- Der Nordstern steht nicht exakt über dem Nordpol.
Er ist etwa um 1o davon entfernt.
Berichtigungstabellen findet man aber im Nautischen Jahrbuch. Dieses Problem ist demnach lösbar.
- Das größere Manko: In der Dämmerung ist der Nordstern kaum sichtbar.
Und nachts ist der Horizont nicht erkennbar. Auch nicht bei Vollmond.
Daher kann man nachts bestenfalls annäherungsweise Sextant-Messungen vornehmen.
Es sei denn, man verwendet einen "Künstlichen Horizont".
Dieser Sextant-Zusatz, der den fehlenden Horizont einspiegeln kann, ist leider ziemlich teuer.
Mittagsbreite
Schiffsmittag, Kulmination, Meridiandurchgang
Der Begriff "Schiffsmittag" hat mit dem normalen "Mittag" nichts zu tun.
Schiffsmittag ist dann, wenn die Sonne exakt im Süden des Beobachters steht.
Gleichzeitig erreicht die Sonne in diesem Moment an diesem Ort ihren Kulminationspunkt, den höchsten Punkt ihres Tagbogens;
sie "kulminiert".
Schiff und Sonnenbildpunkt befinden sich in diesem Augenblick auf gleicher Länge (= auf dem gleichen Meridian).
Deshalb spricht man auch vom "Meridiandurchgang".
Wenn man weiß oder feststellen kann,
- wann die Sonne am Beobachtungsort kulminiert,
und wenn man weiß,
- auf welcher Breite genau im Süden sich der Bildpunkt (BP) der Sonne in diesem Moment befindet,
kann man den eigenen Breitengrad bestimmen.
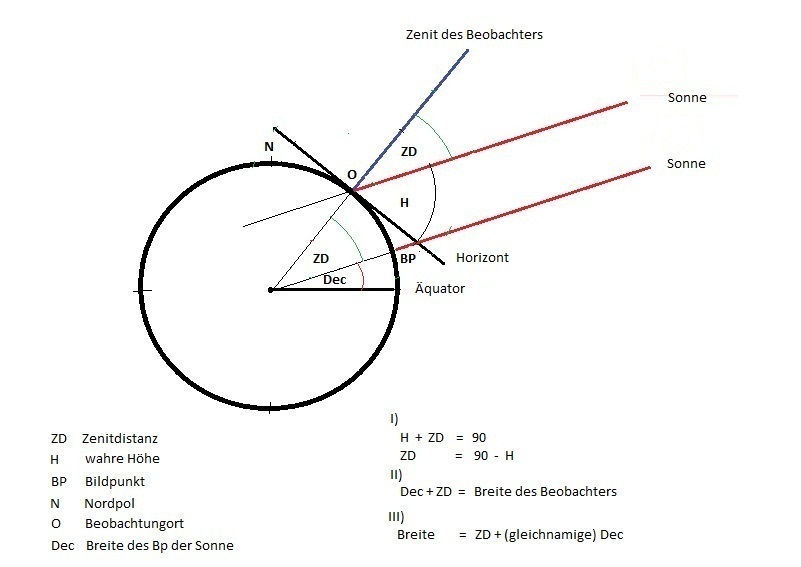
Im folgenden Beispiel liegt der Bildpunkt der Sonne im S des Beobachters, und beide - Beobachterstandort und BP - nördlich des Äquators:
Ähnlich wie bei der Nordsternbreite lässt sich die Mittagsbreite aus den zugehörigen Winkeln am Erdmittelpunkt ableiten.
Sie ergibt sich hier aus der Summe von Zenitdistanz und Deklination:
𝜑 = ZD + δ
Wer sich mit den anderen Konstellationen beschäftigen möchte (gleichnamig - ungleichnamig, BP liegt nördlich des Beobachters),
findet Informationen auf meiner Webseite (s. weiter unten)
Bleibt die Frage, woher man die Deklination der Sonne bekommt?
Aus dem Nautischen Jahrbuch.
Messung in der Praxis
Etwa eine halbe Stunde vor dem geschätzten Schiffsmittag (Kulmination der Sonne) würde man sich mit dem Sextanten an Deck begeben.
Wenn man die Sonne auf den Horizont herunterholt und nach kurzer Zeit wieder durch den Sextanten sieht, stellt man fest,
dass die Sonne nach oben wandert.
Sie ist also auf dem Weg zum Kulminationspunkt.
Sie steigt zunächst relativ rasch.
Wenn sie sich dem Scheitel nähert, verflacht die Tagbogen-Kurve der Sonne; sie ändert die Höhe kaum mehr.
In dieser Phase muss man ständig die Sonne durch den Sextanten betrachten und sie solange auf den Horizont herunterholen,
also am Nonius nachdrehen, solange ihr Bild über (!) dem gespiegelten Horizont im Sextanten steht.
Ab dem Moment, wo die Sonne nicht mehr steigt, nichts mehr machen!
In dem Augenblick, in dem man den Unterrand etwas unter dem eingespiegelten Horizont im Sextanten beobachtet,
beginnt die Kurve zu fallen; die Kulmination ist vorbei.
Wenn man alles richtig gemacht hat, hat man den höchsten Winkel, den Kulminationswinkel, im Sextanten festgehalten.
Wer ausrechnen möchte, muss beachten wie Beobachterposition und Bildpunkt zueinander stehen,
und er muss die Korrekturwerte für die Messung (IB und GB) anbringen.
Der errechnete Wert ist die Breite, auf der sich der Beobachter befindet.
Ist Ihnen aufgefallen, dass bei dieser Breitenbestimmung die tatsächliche Zeit keine Rolle spielt?
Die Mittagsbreite kommt ohne Uhrzeit aus.
Das ist anders bei der Längenbestimmung.
Weil es lange Zeit keine genau gehende Uhr gab, musste man sich über Jahrhunderte hinweg mit der Breite
und Koppelnavigation zufriedengeben.
Mittagslänge
Erst mit Erfindung einer ganggenauen Uhr durch John Harrison (1735) war eine Längenbestimmung möglich.
Wie hängen Zeit und Länge zusammen?
Grundlage von Zeitmessungen ist die Sonne und deren Lauf um die Erde in 24 Stunden.
Der Bildpunkt der Sonne wandert in 24 h einmal um die Erde (um 360o), in 1 h um 15o nach Westen.
Es gibt demnach einen unmittelbaren Zusammenhang zwischen der Position des Bildpunktes (der "Länge" des Bildpunktes) und der Zeit:
1 h entspricht 15o W , 2 h entsprechen 30o W, usw.
Deshalb kann man geographische Länge auch in Zeit ausdrücken.
Daher auch der Name …
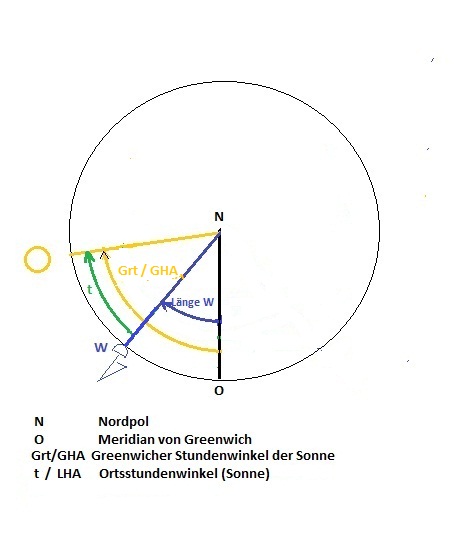
Greenwicher Stundenwinkel (Grt, tGr; Greenwich Hour Angle, GHA)
… für die Längenangabe des Bildpunktes der Sonne.
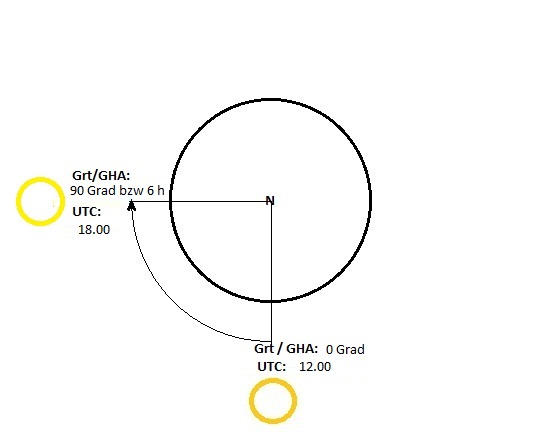
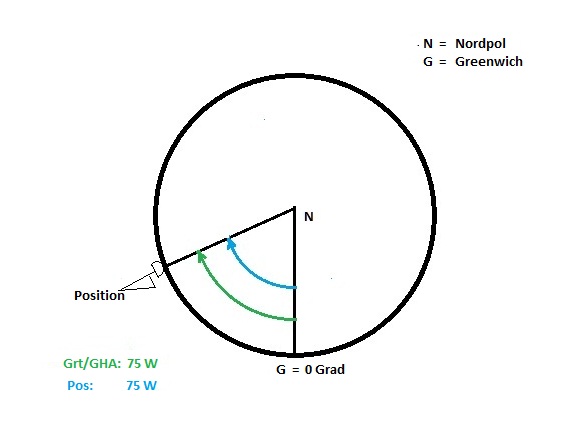
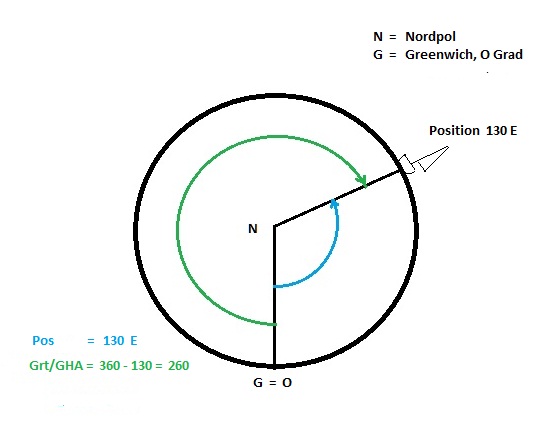
Der Betrachter sieht auf den Nordpol.
Die gelben Kreise symbolisieren die Sonne zu unterschiedlichen Zeiten.
Sowohl die Länge des Bildpunktes der Sonne als auch die Zeit (UTC) werden vom Greenwicher Meridian aus gemessen.
Und dennoch sind die Werte verschieden.
Greenwicher Stundenwinkel (Grt) – Weltzeit (UTC)
Die Sonne kulminiert um 12.00 UTC in Greenwich, auf dem 0-Meridian.
Der Stundenwinkel der Sonne (Grt/GHA) beträgt in diesem Moment aber 0 o, denn ihr Bildpunkt liegt jetzt auf diesem Meridian.
Pro Stunde wandert nun der Bildpunkt der Sonne um 15 ° nach W.
Eine Stunde später, also UTC 13.00, beträgt der Stundenwinkel der Sonne demnach 15 o. 2 h später, UTC 14.00, beträgt ihr Grt 30o, usw.
Diese verschiedenen "Uhren" muss man auseinanderhalten.
Anwendung in der Praxis
Im Vergleich zum theoretischen Hintergrund ist die Handhabung einfach.
Die Tagesbahn der Sonne ist für einen Beobachter ein Bogen am Himmel. Der höchste Punkt dieses Tagbogens heißt "Kulmination".
In den auf- und absteigenden Bogenteilen verändert sich die Position der Sonne in ihrer Höhe rasch.
Aber die Sonne verweilt relativ lange im Scheitelpunkt (etwa 4 min), so dass zwar die Höhe gut gemessen,
nicht aber die Zeit der Kulmination sekundengenau festgestellt werden kann.
Deshalb wendet man einen Kniff an:
- Man hält die sekundengenaue Zeit für eine Höhe im aufsteigenden Teil des Bogens fest, z. B. 1 h vor der angenommenen Kulminationszeit.
- Wenn die absteigende Sonne die exakt gleiche Höhe wieder erreicht, notiert man erneut die exakte Zeit.
Die Zeit der Kulmination ist die Mitte der beiden Zeiten (aus gleichen Höhen).
Voraussetzung ist eine sekundengenau gehende Uhr.
Korrekturwerte erhält man auf See von einigen Kurzwellen-Sendern, z. B. auf 2500 / 5000 / 10000 / 20000 kHz.
Mittagposition (auch Mittagsbesteck)
Sie ergibt sich aus der Kombination von Mittagsbreite und Mittagslänge in einem einzigen Arbeitsgang:
Die Sextantmessung zur Kulmination ergibt die Breite,
die halbierte Zeit aus der Summe der beiden Messungen mit gleicher Höhe ergeben die Länge des Standorts.
Man muss also nacheinander 3 Messungen durchführen.
Bei der dritten Messung stellt man den im aufsteigenden Teil festgehaltenen Winkel erneut ein und wartet,
bis die absteigende Sonne genau diesen Winkel wieder erreicht.
Zeit festhalten!
Solange es keine Computer gab, haben die allermeisten Segler ausschließlich mit diesem Verfahren navigiert.
Denn man erhält mit relativ wenig Aufwand einen Standort.
Nachteilig ist der zeitliche Zwang.
(Übungsbeispiele und zusätzliche Erläuterungen weiter unten)
Beim Tagbogenverfahren erfolgen die Messungen um die Zeit der Kulmination lediglich zu einem besonders günstigen Zeitpunkt.
Die Einhaltung von Zeiten und Sextantwinkeln entfällt.
Darüber u. a. im Folgebeitrag.
- - - - -
Astronavigation einfach, 3. Folge
Die Suche nach dem Standort
In dieser Folge geht es um die mathematischen Überlegungen, die zum eigenen Standort führen.
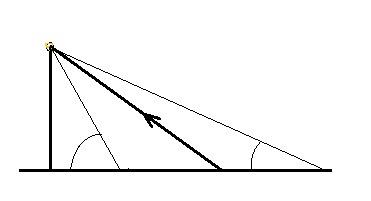
Stellen wir uns vor, wir würden eine Straßenlaterne mit dem Sextanten messen. Ihre Höhe und ihr Fußpunkt sollen bekannt sein.
Wir würden als Ergebnis einen Winkel erhalten, der abhängig ist von der Entfernung zur Laterne.
Daraus ließe sich folgern, dass unser Standort irgendwo auf einem Kreis liegen muss,
der dem Sextantwinkel und dem davon abhängigen Abstand entspricht:
In der Astronavigation heißt die Straßenlaterne "Sonne", ihr Fußpunkt ist der "Bildpunkt",
ihre Position ist bestimmt durch "Breite" (Deklination, δ), und "Länge" (Greenwicher Stundenwinkel, Grt).
Wir sehen uns das an:
mit freundlicher Genehmigung von Herrn Hoffrichter)
Der Kreis, auf dem sich unser Standort befindet, ist sehr groß. Auf einem Seekartenabschnitt wäre er scheinbar eine Gerade.
Sie heißt "Standlinie".
Ein Kreis allein nützt wenig; wir bräuchten zwei Messungen der Sonne. Dann würden sich die Kreise in zwei Punkten schneiden.
Einer davon wäre unsere Position.
Die gelben Kreise symbolisieren jeweils den Bildpunkt der Sonne. Die zugehörigen Standortkreise sind rot bzw. grün.
Die Schnittpunkte der Kreise sind unsere möglichen Standorte.
Der richtige ist jener, wo sich unser Schiff in etwa befindet.
Jetzt fehlen nur noch die Zahlen. Wie wird das ausgerechnet?
Das Nautische Dreieck
Wir erinnern uns, dass alle Strecken auf der Erdkugel eigentlich Winkel sind, die am Erdmittelpunkt gemessen werden.
Die Äquatorebene verläuft durch den Erdmittelpunkt, ebenso die Achse Südpol – Nordpol. Beide bilden einen 90° - Winkel zueinander.
Die Deklination δ, der Winkel zum Bildpunkt der Sonne, ist ein Teil dieses 90°- Winkels. Der Ergänzungswinkel zu 90°, der Komplementärwinkel, beträgt 90 – δ. Die Seiten sind jeweils der Radius des Erddurchmessers.
Wenn man drei Elemente eines Dreieckes kennt, kann man die anderen Elemente berechnen.
Kennt man δ und r, kann man die Streckenlänge von δ auf der Kugeloberfläche und jene von 90 - δ berechnen.
Das Verfahren - Komplementärwinkel minus Bestimmungs-Winkel) - gilt im Prinzip für alle Strecken des Nautischen Dreiecks.
Es ist Grundlage aller Überlegungen zur Standortberechnung.
X ist der Bildpunkt der Sonne.
Er wird definiert durch die Deklination δ (Breite) und den Stundenwinkel Grt (Länge).
Beide kennen wir (Nautisches Jahrbuch, UTC).
Z ist der Beobachter.
Seine Breite ist 𝜑.
Seine Länge ergibt sich aus der Summe von Grt und τ (tau). Tau wird berechnet.
Nur in bestimmeten Konstellationen ist tau identisch mit dem LHA.
Der Ortsstundenwinkel (LHA) wird gemessen vom Schiffsort nach W zum Bildpunkt der Sonne.
Die Berechnung des LHA ist in bestimmten Konstellationen etwas kompliziert.
Das muss uns in diesem Zusammenhang nicht interessieren.
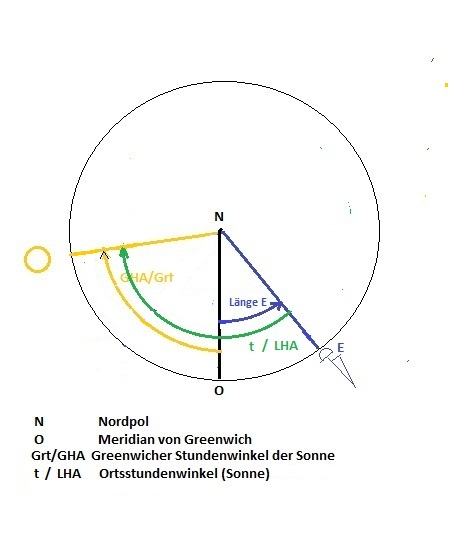
Nachtrag:
Wenn die Sonne westlich des Beobachterstandortes beobachtet wird, entspricht der Winkel tau dem Ortsstundenwinkel (t, LHA).
Wird die Sonne im Osten beobachtet, ergibt sich tau aus 360 ° (von 0° aus gerechnet) - t.
Einleuchtende Skizzen finden Sie bei
ziemlich weit unten.
Die Streckenlänge der dritten Seite Z – X ergibt sich aus der Sextantmessung (Höhe, h), nämlich als 90 – h.
Der Winkel Az heißt Azimut.
Es ist der Peilwinkel zum Sonnenbildpunkt. Azimut und Standlinie bilden einen 90° - Winkel.
Wir kennen demzufolge:
- die Seite N - X (90 – δ) und dazu den Winkel am Nordpol (Grt)
- Wir kennen außerdem die Länge der Seite Z – X (90 – h).
Aber nicht ihre Richtung.
Es ist der Radius eines Kreises, des "Standortkreises", um den Bildpunkt der Sonne (in der folgenden Skizze grün eingezeichnet).
- 𝜑 und τ wollen wir berechnen.
Nun messen wir die Sonne ein zweites Mal.
Nehmen wir an, unser Schiff liegt in einer Flaute still und die zweite Sextantmessung erfolgt am Nachmittag:
Dann würde sich ein zweites Dreieck aufspannen, von dem wiederum die Seite X´- P bekannt ist.
Die Seite Z - X ist erneut der Radius eines Kreises (rot eingezeichnet).
P in der Skizze heißt Pol. Besser wäre die Bezeichnung N = Nordpol.
In gezeigten Fall haben beide Dreiecke eine gemeinsame Seite: Z – P (Beobachter – Pol).
Wenn X und X´ und die Standkreise dazu bekannt sind, kann man in einem langwierigen mathematischen Rechengang
den Schnittpunkt dieser Kreise berechnen.
Ergebnis ist Z, der Ort des Beobachters.
Wenn sich das Schiff bewegt, kommt eine Versegelungsrechnung hinzu. Auch das ist mathematisch lösbar.
Als erster hat diese Aufgabe Carl Friedrich Gauß (1777 – 1855) gelöst.
Die Methode von Gauß wurde dennoch in der Navigation nie verwendet, weil der Rechengang sehr aufwendig ist.
Für einen PC aber ist dies kein Problem, wenn erst einmal programmiert.
Helmut Hoffrichter hat die Methode von Gauß wieder entdeckt.
Die Zwei-Höhen-Methode
Zurück zum Nautischen Dreieck.
Es ließen sich alle seine Elemente berechnen, wenn Z, der Beobachtungsort, bekannt wäre.
(Allerdings müsste man dann auch nicht mehr rechnen.)
Der französische Admiral Marq Saint Hilaire hatte die Idee (1875), so zu tun, als kenne man den Standort.
Für diesen angenommenen Standort ließe sich der Höhenwinkel zur Sonne und das Azimut berechnen;
Länge und Breite sind mit dem angenommenen Standort bereits festgelegt.
Wenn man die tatsächlich gemessene Höhe (Ho) mit dem ausgerechneten Winkel (Hc) vergleicht,
würden sich drei Möglichkeiten ergeben:
1) Die gemessene Höhe (Ho) und die für den Koppelort berechnete Höhe (Hc) sind identisch.
Dann würde der Schiffsort auf der angenommenen Standlinie liegen. Dieser Fall ist eher unwahrscheinlich.
2) Der gemessene Winkel ist kleiner; die Standlinie würde vom Bildpunkt der Sonne weiter entfernt sein als der Koppelort.
Der Winkel zu einer Straßenlaterne wird kleiner, je weiter entfernt man vom Fußpunkt der Laterne aus misst.
3) Der gemessene Höhenwinkel ist größer, als der vorberechnete.
Dann würde die Standlinie näher zum Bildpunkt der Sonne liegen.
Der Abstand Hc (berechnete Höhe) - Ho (beobachtete Höhe) auf dem Azimutstrahl heißt Intercept.
Zeichnerische Lösung
Man nimmt kariertes Rechen- oder Millimeterpapier und legt einen Maßstab fest, z. B. 2 Kästchen = 1 sm.
Dann trägt man vom Koppelort aus das Azimut an und versieht es mit einem Richtungspfeil.
Wenn der gemessene Höhenwinkel größer ist als der ausgerechnete, z. B. 1´, liegt die Standlinie um 1 sm näher zur Sonne hin
als der eigene Koppelort.
Zwei zeitlich deutlich auseinander liegende Sextantmessungen ergeben zwei Standlinien, die sich schneiden.
Der Kreuzungspunkt ist der "wahre" (richtige) Standort.
Schiffe bewegen sich. Wenn die erste Messung am Vormittag erfolgt, die zweite am Nachmittag, müssen Kurs
und zurückgelegte Strecke (Versegelung) einbezogen werden:
Die rechte Seite obiger Skizze zeigt den Koppelort I mit zugehörigem Azimutstrahl I, Intercept I und Standlinie I.
Das Schiff bewegt sich von Koppelort I zu Koppelort II.
Die Standlinie I wird mitverschoben (Versegelung),
Im Koppelort II erfolgt die zweite Messung mit Azimutstrahl II, Intercept II und davon abgeleitet Standlinie II.
(Dieses Mal ist der Messfehler im Beispiel geringer, aber wiederum ist der Messwinkel kleiner als der berechnete Winkel.)
Der Schnittpunkt von Standlinie II und versegelter Standlinie I ergibt den wahren Standort zum Zeitpunkt der 2. Messung.
Der Rechenaufwand ist – trotz zeichnerischer Lösung – noch immer hoch.
Denn man muss den Koppelort und den von ihm abgehenden Azimutstrahl nach wie vor berechnen
(vor der Taschenrechner-Zeit mit Winkelfunktionen und Logarithmentafeln).
Vereinfacht wurde das Verfahren erst, als das amerikanische Hydrographic Office (H. O.) die Werte
für alle ganzgradigen Breiten und Ortsstundenwinkel (LHA) vorausberechnete und als mehrbändiges, dickes Nachschlagewerk
(meines Wissens im 2. Weltkrieg) herausbrachte, die sog. HO-Tafeln.
Am beliebtesten wurden die für die Air Force entwickelten "Sight Reduction Tables for Airnavigation".
Allein im Bd. III, für die Breiten 40° - 89°, sind (360° * 49° =) 17.640 Kreuzungspunkte von Breite und LHA
mit den möglichen Deklinationen der Sonne von 0° - 29° (17640 * 29 = ), also 511560 Eingänge, vorberechnet.
Für die Anwendung gilt:
Der Rechenort muss so gewählt werden, dass er möglichst nahe am Koppelort liegt.
- Man schlägt die Seite des nächstgelegenen ganzgradigen Rechenortes auf,
- geht anschließend auf den LHA (Ortsstundenwinkel)
- und sucht in der Tabelle die ganzgradige Deklination.
In der Tabelle findet man nun die vorausberechnete Höhe (Hc) und das Azimut für diesen Rechenort.
- Nun zeichnet man , wie oben vorgeführt, die entsprechenden Werte an.
An die Stelle der Koppelorte treten ganzgradige Rechenorte.
- Die zweite Messung ergibt eine zweite Standlinie. Der Schnittpunkt der beiden Linien ist die eigene Position.
Mit dem Sextanten hat man Jahrhunderte auf See navigiert.
Erst mit der Einführung des GPS in den 1980er Jahren verlor der Sextant seine Bedeutung.
Nicht einmal als Backup ist er heute noch notwendig.
Dennoch erlebt die Arbeit mit dem Sextanten gegenwärtig eine Wiederbelebung.
Allerdings in Kombination mit programmierbaren Taschenrechnern, die es ebenfalls etwa ab 1980 gibt.
Seit dieser Zeit wird die Intercept-Methode, wie die Methode von St. Hilaire auch genannt wird, programmiert,
so dass weder das Nachschlagen im Nautischen Jahrbuch noch in den HO-Tafeln,
noch die zeichnerische Auswertung mehr nötig sind.
Taschenrechner ermöglichen es, auch andere Rechenwege zu programmieren.
Eines aber bleibt dabei gleich:
Zwei zeitlich deutlich auseinander liegende Messungen führen zu zwei sich schneidenden Standkreisen (Standlinien),
deren Schnittpunkt die eigene Position ergibt.
Die Zwei-Höhen-Methode enthält systemimmanente Fehler:
Fehlerbetrachtung der Zwei-Höhen-Methode
- Wenn eine der beiden Beobachtungen grob falsch ist, liegt auch das Ergebnis deutlich daneben.
- Eine Standlinie ist keine scharfe Linie, sondern ein Streifen von mindestens +/- 1 sm, also 2 sm Breite.
Wenn sich zwei Streifen schneiden, entsteht ein Parallelogramm, im besten Falle ein Quadrat, in dessen Inneren sich irgendwo
die Beobachterposition befindet.
Das Parallelogramm wird sehr lang, wenn sich die Standlinien unter spitzen (oder stumpfen) Winkeln schneiden.
Am "Problem der schleifenden Schnitte" ändert auch ein Rechenprogramm nichts, selbst wenn es in scheinbarer Genauigkeit
mehrere Stellen hinter dem Komma ausgibt.
Deshalb muss zwischen den beiden Messungen ein ausreichender zeitlicher Abstand liegen,
damit spitze Schnittwinkel vermieden werden.
4 Stunden, sagen Praktiker.
Eine dritte Standlinie verkleinert die Fehlerfläche deutlich:
Ergebnis: Je mehr Standlinien (Messungen), desto genauer der Standort.
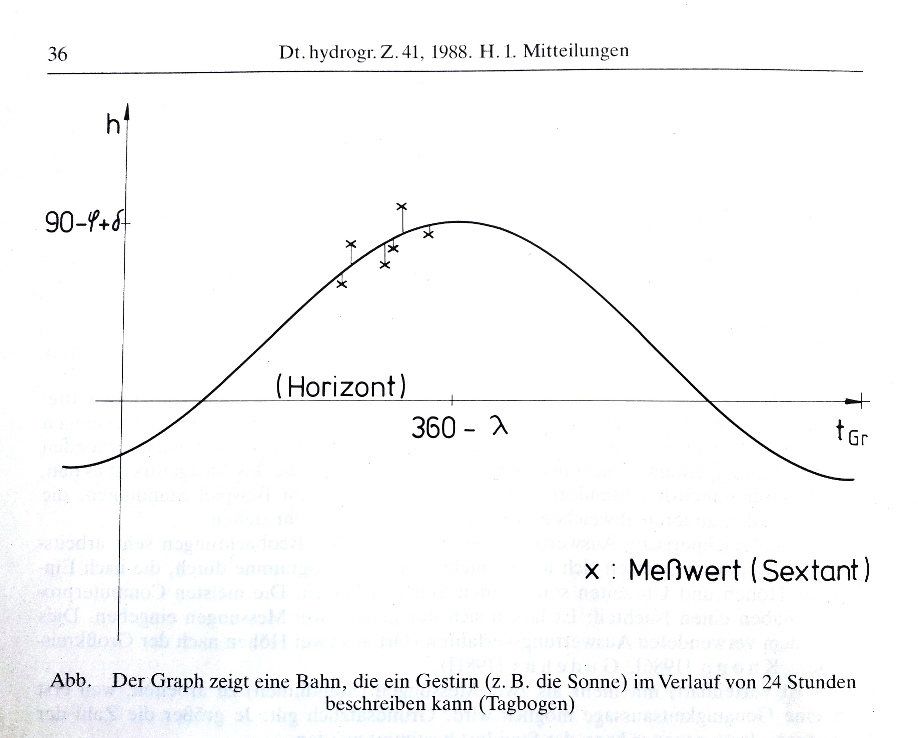
Das Tagbogenverfahren
… von Dr. Ralf Lampalzer (veröffentlicht 1988 in der Deutschen Hydrographischen Zeitschrift) arbeitet
mit einer Vielzahl von Messungen.
Es verfolgt einen völlig neuen Ansatz und ist ein mathematisches, computergestütztes Verfahren,
dessen Name sich von der Sonnenbahn über dem Horizont, dem Tagbogen, ableitet.
Jeder Ort hat eine spezifische Tagbogenkurve.
Mit Hilfe mehrerer Messungen wirtd die Sonnenbahn dieses messortes rekonstruiert.
Vom ermittelten Tagbogen rechnet der Computer auf die Positiondes Beobachters zurück.
Was im PC vorgeht
Bei wirklich genauen Messungen müssten alle Messwerte auf der Tagbogenkurve des Messortes liegen.
Weil die einzelnen Messungen aber mit Fehlern behaftet sind (Schiffsbewegungen z. B.), liegen sie darüber oder darunter.
Nun wird die Kurve mit der kleinsten Abweichung zu den Messungen gesucht.
Dort wo die Abweichung am geringsten ist (Minimum) liegt der gesuchte Ort, der Standort.
Die Suche nach dem Minimum erfolgt über das sog. Gradienten-Abstiegs-Verfahren
und nähert sich der Lösung (dem Ort mit der geringsten Abweichung) schrittweise.
Der Computer wiederholt den Rechenprozess mehrfach mit den jeweils verbesserten Startwerten,
solange, bis die gefundene Position sich nicht mehr ändert (außer in der 4. Stelle nach dem Komma.)
Erweiterungen
- Es wäre möglich, die zwischen den Messungen versegelte Strecke einzubeziehen.
- Wenn man die Mittel der Fehlerrechnung hinzunimmt, kann man mit Hilfe eines Ausreißertests
grob verfälschende Messungen eliminieren.
- Und man könnte einen Vertrauensbereich des Ergebnisses berechnen, so dass der Navigator sich nicht auf sein Gefühl
verlassen muss, sondern – ähnlich wie oben – die Ausdehnung der Fehlerfläche genannt bekommen würde.
Anwendung
Einzugeben sind lediglich die Variablen, nämlich Datum, Augeshöhe (Ah = Höhe des Messpunktes über dem Wasserspiegel),
Messzeit und Messergebnis.
5 Messungen innerhalb einer Viertelstunde, dann eine Viertelstunde Pause und anschließend erneut 5 Messungen
ergeben einen relativ sicheren Standort.
Download
Ein Download des Tagbogenverfahrens steht allen Interessierten kostenlos zur Verfügung unter
Voraussetzung ist eine Excel-App.
- - - - -
II. Astronavigation für Einsteiger
1. Überblick
2. Sextant, Sonne schießen, Berichtigungen, Stellarium
3. Nordsternbreite
4. Mittagsbreite
Das vorausgehende Kapitel "Astronavigation einfach" ist identisch mit der Artikelfolge in segeln, Juli / Sept / Okt 2024.
Diese Texte wiederum sind im Prinzip eine Neubearbeitung der nachfolgenden Kapitel.
Deshalb wiederholen sich im Folgenden die Grundideen.
Allerdings sind sie in "Astronavigation für Einsteiger" ausführlicher dargestellt; vor allem findet man Rechenbeispiele.
Eigentlich wurde das Zeitalter der Astronavigation abgelöst durch die Satelliten-Navigation.
Denn auch mit einem Hand-GPS kann man weltweit seine Position feststellen.
Bei einem Gewitter kann es allerdings passieren, dass die gesamte Elektronik, also auch der Hand-GPS, ausfällt.
Man müsste ihn wenigstens in eine Metallkassette gesteckt haben.
Wenn man ehrlich ist, ist es einfacher, genau dies zu tun, als sich das Wissen der Astro-Navigation anzueignen.
Dieses Wissen ist allerdings auch Prestige-Können eines Kapitäns:
Wer eine Yacht hat und Hochsee-Segeln betreibt, will wissen, wie man mit einem Sextanten die eigene Position auf See bestimmt.
Das erst macht ihn zu einem wirklichen Kapitän.
Aber auch ganz ohne Prestige: Astronavigation ist höchst interessant.
Was braucht man?
- Einen Sextanten
Es muss kein hochwertiger Sextant sein. Ein Kunststoff-Sextant tut es auch und sie sind besser als gerne dargestellt.
Test bei Helmut Hoffrichter: zephir-yacht.com/astronnomische-navigation-2/sextantentest-2
Der Davis Mark 15 kostet zwischen 280,- und 325,- € (April 2024).
Ein großer Vorteil von Kunststoffsextanten ist - entgegen anderer Behauptungen - dass sie leicht sind.
- Wissen muss man, wie man den Sextanten bedient, um die Sonne zu "schießen".
- Ein künstlicher Horizont zum Üben ist ebenfalls nötig. (Er ersetzt den Horizont auf See.)
Man kann ein Zusatzinstrument für viel Geld erstehen.
Um zu Hause zu üben, eignet sich auch ein Teller mit Wasser oder Öl als Spiegel für die Sonne.
- Die Uhrzeit zum Messzeitpunkt muss sekundengenau festgehalten werden.
Ein Partner ist dabei hilfreich.
- Die Rechenarbeit kann man einem Computer-Programm überlassen (s. weiter unten).
- Sextant
Der Sextant ist ein sehr genaues Winkel-Messgerät.
Sextanten werden so genannt, weil der Gradbogen an ihrer Unterseite ein Sechstel eines Kreises (60 o) groß ist.
Der Vorteil eines Kunststoffsextanten ist (natürlich neben dem deutlich niedrierem Preis) das geringere Gewicht.
Wer Schulter- oder Ellenbogenprobleme hat, wird mit den größeren Gewichten kaum zurecht kommen.
Ich würde in jedem Falle erst mit einem Kunststoffsextanten beginnen.
Preise:
- Davis, "MK 15" ~ 325,- € (August 2023 bei SVB)
- Davis "Mark 25 DeLuxe" ~ 380,-
Wer sich eingehend mit der Astronavigation beschäftigt, wird einen hochwertigen Sextanten erwerben.
Cassens & Plath empfiehlt bei Schulterproblemen das Camcorder Schulterstativ von Kaiser. (~ 45 €, 2023)
Der Sextant kann zusätzlich mit einem Künstlichen Horizont ("Libelle") ausgerüstet werden.
Dieser ist in der Nacht notwendig, denn dann ist die Kimm (Horizont) nicht exakt zu erkennen, auch wenn es so scheint.
Erst mit dieser Zusatzausrüstung sind Messungen des Nordsterns (Nordsternbreite) oder anderer Sterne nachts machbar.
- Künstlicher Horizont, Libellenaufsatz (Cassens & Plath) ~ 850,- € (Aug. 2023)
- "Sonne schießen" (Abstand Kimm – Sonnenunterrand messen)
Dazu muss man wissen, wie man mit einem Sextanten umgeht: Messung, Fehlerberichtigungen. (s. 3. Sextant)
Für die
- Auswertung der Messungen
gibt es verschiedene Möglichkeiten:
Auswertung mit Rechner
Am einfachsten ist, sich einen Rechner mit einem astronomischen Rechenprogramm zu kaufen.
Gute Programme enthalten alle astronomischen Berichtigungswerte.
Es gibt aber auch kostenlose Freeware-Programme.
Man misst die Höhe eines Gestirns, gibt die Werte ein, misst 4 h später erneut, gibt ein und erhält die eigene Position.
Nachteilig ist, dass man ~ 4 h warten muss, um einen brauchbaren Standort zu bekommen.
Dieser lange zeitliche Abstand ist beim Tagbogenverfahren nicht notwendig.
"Das Verfahren ermöglicht bei den typischen Messfehlern (Sextant freihändig gehalten, Seegang) von ca. 2'
eine für praktische Zwecke brauchbare Standortbestimmung in etwa 45 Minuten mit 10 Messungen." (Dr. Ralf Lampalzer)
Dieses Verfahren ist unter "Downloads" (auf dieser Webseite) kostenlos verfügbar.
Händische Auswertung
Wenn man nicht mit einem Rechner arbeitet, ist es deutlich komplizierter.
Man braucht unterrschiedliche Tafelwerke, um bestimmte Dinge nachzuschlagen und das nötige Wissen,
das man sich am besten in einem Astro-Lehrgang aneignet.
Normalerweise wird das Verfahren: "Standortbestimmung aus zwei Messungen" vermittelt.
- - - - -
2. Sextant, Sonne schießen, Stellarium
2.1 Sextant
2.2 Messfehler-Berichtigung
2.3 Messen einer Gestirnshöhe
2.4 Beschickungen
2.5 Künstlicher Horizont
2.6 Teller mit Wasser als künstlicher Horizont
2.7 Stellarium
2.8 Begriffe
2.1 Sextant
Wikipedia:
- Teile des Sextanten
Limbus Gradbogen mit Winkelskala
Alhidade beweglicher Zeigerarm
Index Zeigerstrich
Trommel Einstellmechanismus zum Ablesen der Grade;
eine (ganze) Umdrehung der Mikrometerschraube verschiebt die Alhidade um 1 o
Nonius Hilfs-Maßstab, vergleichbar mit Rechenschieber;
er gestattet das Ablesen von Zwischenwerten
Indexspiegel Spiegel auf der Alhidade und mit ihr beweglich
Horizontspiegel der feste, unbewegliche Spiegel (halb verspiegelt)
Blendgläser Schattengläser, verdunkelte Gläser
Typen von Sextanten
- Traditioneller Halbsichtspiegel
Eine Hälfte des Horizontspiegels versilbert (verspiegelt).
Es gibt nicht nur diesen traditionellen Sextanten. Cassens & Plath führt zusätzlich auf:
- Vollsichtspiegel (umgangssprachlich: Vollsicht-Sextant)
- Freisichtspiegel
Ich persönlich habe einen "klassischen" Sextanten und komme gut damit zurecht.
Wichtig ist, dass man das übliche Teleskop (4 x 40) wählt und sich nicht auf stärkere Vergrößerungen einlässt (6 x 30).
Dann ist das Finden der Sonne deutlich schwieriger.
Ich weiß nicht, ob Vollsicht- oder Freisicht- Sextanten wirklich einfacher zu handhaben sind.
Ich würde mit einem Kunststoff-Sextanten beginnen und beim gleichen System bleiben, wenn man zurechtgekommen ist.
Oder die verschiedenen Typen im Fachgeschäft ausprobieren!
Der klassische Trommelsextant
An einem Metallrahmen ist ein beweglicher Zeigerarm angebracht, der auf dem Gradbogen unten, der Grad-Skala,
den gemessenen Winkel anzeigt.
Um den Winkel wirklich genau einzustellen (auf 10tel Minuten), dreht man an der Mikrometerschraube links.
(Das macht der Navigator gerade im obigen Bild).
Im Sichtfenster des Gradbogens können die ganzen Grade des gemessenen Winkels, am Nonius die Minuten und 10tel-Minuten
abgelesen werden.
Es ist die gleiche Ablesetechnik wie bei einem Messschieber.
Funktionsweise
Wenn man durch das Teleskop schaut, geht der Blick durch den "Horizontspiegel".
Dieser besteht halbseitig aus Normalglas, die andere Hälfte ist verspiegelt. (Das ist im Foto gut zu erkennen.)
Wir setzen die Gradzahl auf 0°. Mit Hilfe einer Sperrklinke kann der Zeigerarm arretiert werden.
(Beim Sextanten im Bild ist es ein drehbarer Knopf unterhalb des Grad-Sichtfeldes.)
Auch die Minutenskala stellen wir auf 0,0´; d. h. der Null-Strich der (drehbaren) Minuten-Skala links muss exakt mit dem Nullstrich
der (festen) Nonius-Skala fluchten.
Der Sextant zeigt nun 0° 0,0´.
Nun richten wir (wie der Navigator oben) den Blick durch das Teleskop auf den Horizont.
Man sieht durch das Fensterglas des Horizontspiegels die eine Hälfte des Horizonts.
Die andere Hälfte wird ergänzt durch die Reflexion der Lichtstrahlen, die vom Horizont kommend
vom Indexspiegel auf die Rückseite des Horizontspiegels geworfen und von dort ins Auge des Betrachters geleitet werden.
Ergebnis:
Wir sehen eine durchgehende Horizontlinie, denn der eingespiegelte Horizont setzt den tatsächlich gesehenen Horizont
scheinbar nahtlos fort.
Wenn der Zeigerarm nicht bei 0° stehen würde, sondern z. B. bei 60 °,
würde ein Objekt eingespiegelt, das sich dort (60° über dem Horizont) befindet, z. B. die Sonne.
Dann würden wir links den Horizont und rechts die eingespiegelte Sonne wahrnehmen.
Sonne schießen
Vorneweg eine Warnung:
Der Sextant hat ein Fernrohr (Teleskop), durch das der Navigator auf dem Bild gerade blickt.
Wenn man mit einem Fernrohr ungeschützt in die Sonne schaut, wird das Auge geschädigt.
Daher niemals den Sextanten ohne Filter (Schattengläser) benutzen!
Das Teleskop stellt man scharf wie jedes Fernrohr, durch Drehen am Okular.
Zuerst das prinzipielle Vorgehen:
Wir setzen die Sonne mit ihrem Unterrand auf den Horizont, d. h. Sonne und Horizont berühren sich im kleinstmöglichen Punkt.
(Der häufigste Messfehler ist, dass Sonne und Horizont eine kleine Berührungslinie bilden.)
In diesem Moment muss die sekundengenaue Uhrzeit genommen werden.
(Jede unrichtige Sekunde würde die Position um ~ 463 m nach W oder E verfälschen.
Erdumfang 40.00 km : 24 h : 60 min : 60 sec = 0.4629 km).
Der am Gradbogen und Nonius ausgelesene Wert ist die "Höhe" der Sonne zum Messzeitpunkt.
Nun zur Praxis:
Der Partner beobachtet seine Handy-Uhr oder die Zeitanzeige am PC.
Als erstes klappen wir sowohl vor den Horizontspiegel als auch vor den Indexspiegel zwei Filter
und suchen die Sonne durch das Fernrohr bei 0°-Stellung am Gradbogen.
Ist die Sonne noch immer zu hell, nehmen wir den dritten Filter dazu.
Dann betrachten wir den Horizont.
Ist das Sichtfeld zu dunkel, verringern wir die Zahl der Schattengläser vor dem Horizontspiegel.
Die Gradzahl ist 0°, wie oben.
Jetzt beginnt der Messvorgang.
Man richtet das Fernrohr auf den Horizont unterhalb der Sonne.
Nun bewegt man den Zeigerarm langsam von uns weg, kippt also den Indexspiegelnach oben, so weit, bis die Sonne erscheint.
Wenn sie möglichst knapp über dem Horizont steht, lassen wir die Feststell-Klemme einrasten.
Durch Drehen am Nonius (wie der Navigator im Bild) holen wir die Sonne weiter auf den Horizont herab, so,
dass sie ihn mit dem Unterrand gerade berührt.
Dabei pendeln wir den Sextanten etwas. Der tiefste Punkt der entstehenden Pendelkurve ist entscheidend.
Wenn die Sonne den Horizont beim Pendeln „küsst“, rufen wir „Jetzt!“; der Partner notiert die Uhrzeit sekundengenau.
- Ablesen von Messwerten
Grad Der Zeigerarm hat über dem Gradbogen (Limbus) ein Fenster. Dort ist ein Messstrich angebracht.
Der darunterliegende Wert zeigt die gemessenen Grade an.
Liegt der Zeiger zwischen zwei Gradstrichen, gilt der kleinere Wert (rechts vom Strich).
Die Zwischenwerte (Minuten) liefert die Messtrommel.
Minuten Der Nullstrich der Noniusskala ist die Markierung für die Minutenablesung.
Liegt der Nullstrich zwischen zwei Minutenwerten, gilt wiederum der kleinere Wert.
Den Zwischenwert liefert die Noniusskala.
Sekunden, Zehntel Bei einer Schublehre kann man auf Hundertsel genau ablesen, beim Nonius eines Sextanten
nur auf Zehntel genau.
Man liest auf der Noniusskala den Teilstrich ab, der mit einem Strich auf der Minutenskala der Messtrommel fluchtet.
Die Gradeinstellung auf der Skala des Sextanten zeigt 59 ° plus etwas:
Auf Trommel lesen wir 5´ plus etwas:
Dort wo die Teilstriche der Nonius-Skala (rechts) mit den Minuten-Teilstrichen (links) fluchten,
ist der 10.el Wert zu finden: 0,4´ .
Gesamt: 59 ° 05,4 '
- - - - -
2.2 Messfehler-Berichtigung
Indexberichtigung (auch Indexbeschickung, IB): rechnerische Berücksichtigung kleiner Fehler
Der Fehler selbst heißt Indexfehler (auch Index-Error, IE)
Das ist zu tun:
Man stellt mit Hilfe des Zeigerarmes (Alhidade) und der Mikrometerschraube den Messwinkel des Sextanten auf 0o 0,0´.
(Der Nullstrich der Nonius-Skala muss mit dem Nullstrich der Mikrometerschraube fluchten.)
Nun richtet man den Sextanten auf den Horizont (oder eine andere waagrechte Linie möglichst weit entfernt).
Sextant lotrecht halten!
Die beiden Hälften des Horizonts (eine Hälfte direkt sichtbar, die andere Hälfte reflektiert durch Indexspiegel etc.)
müssten eine durchgehende Linie bilden. Meist aber entsteht eine Stufe.
Mit Hilfe der Mikrometerschraube wird nun ein durchlaufender Horizont erzeugt.
Ein Blick auf den Zeigerstrich der Mikrometerschraube zeigt uns anschließend den Messwert.
Nehmen wir einmal an, der Messwert ist 1o (der Zeigerstrich steht links von der Null-Markierung, die Nonius-Skala zeigt 0,0´).
Der Messwert müsste aber 0o sein. Der Sextant misst also um 1o zu viel.
Um dieses 1o muss korrigiert, nämlich abgezogen werden.
Nehmen wir an, bei einer Gestirnsmessung zeigt dieser Sextant 45o 30´ an,
dann ist der berichtigte Wert (45o 30´ - 1o = ) 44o 30 ´.
Wenn der Sextant mehr misst (1o anstelle von 0o) muss um diesen Betrag der Messwert vermindert werden, ist also abzuziehen.
In der Regel handelt es sich um Minuten, nicht um Grad.
Bsp. 2:
Skala auf 0 o 0,0 ´. Blick auf den Horizont (oder eine andere weit entfernte waagrechte Linie, einen Dachfirst z. B. ).
Wenn wir die kleine Stufe, die wir beim Sehen durch Drehen an der Mikrometerschraube egalisieren, zeigt der Wert 3.2´.
Der Sextant misst anstelle 0 Grad 3,2 Minuten. Er misst also um 3.2 Minuten zu viel. (IE = + 3.2 ´)
Um diesen Betrag müssen alle sich anschließenden Gestirnsmessungen vermindert werden (Indexberichtigung, IB: - 3.2)
Werte links von der Null-Markierung sind positiv. (Es sind die Winkelwerte des Gestirns über dem Horizont.)
Wenn der Indexerror (IE) positiv ist (im Beispiel + 1o), muss abgezogen werden: IB = - 1o.
Die logische Folgerung:
Werte rechts von der Null-Markierung sind "negativ". Um diesen Betrag misst der Sextant zu wenig.
In der Korrektur muss um diesen Betrag addiert werden.
Negativer IE : zu allen Ablesungen addieren.
Positiver IE: subtrahieren.
... so steht es in den Lehrbüchern.
Besser ist, den Vorgang zu durchschauen.
Bsp. 3
Stellung des Sextanten wie oben auf 0o 0,0´.
Der Horizont wird angepeilt.
Es gibt eine kleine Stufe. Wir korrigieren durch Drehen an der Mikrometerschraube.
Ergebnis: Der Zeigerstrich am Limbus steht kaum merklich rechts von der Nullmarkierung.
Der Sextant misst also zu wenig! Denn es müssten ja 0o sein. (Zeiger genau auf der Null-Markierung).
Es sind 55, 4 ´.
Wenn wir nachdenken, sind das fast 1 o .
Kaum merklich rechts von der Nullmakrierung kann unmöglich ein ganzes Grad sein!
Da stimmt etwas nicht. Wo liegt der Fehler?
Die Skala des Sextanten geht von der Null-Markierung nach links (Plusbereich) und nach rechts (Minusbereich) in 1 o - Schritten:
... 3 - 2 - 1 - 0 - 1 - 2 - 3 ...
Die Minuten-Einteilung an der Trommel zeigt eine andere Einteilung.
Entscheidend ist die feste, sich nicht bewegende -.0 - Markierung
57
58
59
0 .0
1
2
3
Dreht man die Trommel nach oben hinten (Plus-Richtung) bewegt sich die Minutenskala nach 1, 2, 3 ..
59
0
1 .0
2
Drehen wir die Schraube am Nonius (Minutenskala) in die andere Richtung (nach "Minus") erscheint nicht 1, 2, 3 sondern 59, 58, 60,
58
59 .0
0
1
Nach 0 (Null) darf aber nicht - 59 kommen, sondern - 1.
- 1 erhält man, wenn man 59 von 60 abzieht.
Bei den Minuten - Minuswerten muss man die Werte von 60 abziehen, um den Indexfehler zu erhalten.
Bleiben wir bei dem Bsp. 3:
Die Anzeige 55,4 bedeutet demnach 60 - 55,4 = 4.6 ´
Und zwar "Minus", weil rechts vom Grad-Teilstrich: - 4.6 (Indexerror, IE)
Als Berichtigung müssen alle Messungen mit diesem Sextanten um diesen Wert aufgestockt werden.
Indexberichtigung (IB) also: + 4,6`.
Tipp
Schöner wäre es, man würde grundsätzlich keine Minus-Werte erhalten.
Das kann man dadurch erreichen, dass man den Horizont-Spiegel entsprechend einstellt, manipuliert.
Bevor man die Spiegel justiert, sollte man das Handbuch, das jedem Sextanten beiliegt, konsultieren.
In Kürze:
Man stellt auf 0 o 0.0 ´, sucht sich eine weit entfernte horizontale Gerade, sieht durchs Okular, und registriert die kleine Stufe
in der horizontalen Geraden.
Mit Hilfe des mitgelieferten kleinen Imbusses, dreht man nun - während man weiter durchs Okular schaut -
abwechselnd an den beiden Schrauben, die den Horizontspiegel (den unteren Spiegel, den mit der verspiegelten Hälfte) justieren.
Ideal wäre, wenn bei fluchtender Linie im nachfolgenden Test tatsächlich 0 o 0.0 ´ herauskommen würde.
Wenn nicht, sollte man den Spiegel so justieren, dass der IE im positiven Bereich, also links von der Null-Markierung, zu liegen kommt.
- Beispiel einer Indexberichtigung und anschließender Sonnenunterrands-Messung
Bei der Überprüfung (Horizontansicht) steht der Gradstrich auf 0o, die Mikrometerschraube knapp links vom Nullstrich
zwischen 1` und 2`, der Nonius fluchtet bei .6
Der Sextant misst also zu viel, der Indxsfehler ist "positiv":
Indexfehler (IE): + 1.6 ´
Um diesen Betrag muss korrigiert, hier abgezogen werden.
Indexberichtigung (IB): - 1,6
Dann Höhenmessung, z. B. Sonnenunterrand mit: 60o 45,3`
Rechnung:
Sextantablesung: 60o 45,3`
IB - 1,6
Kimmabstand 60o 43,7`
Fehlerquelle ist Kopfrechnen. Daher immer schriftlich oder mit Rechner!
- Einstellung der Spiegel
Wird der Indexfehler zu groß (M. Blewitt spricht von 3´, Knopp von 7´), sollten die Spiegel neu justiert werden.
Bei zu häufiger Betätigung leiern allerdings die Schrauben der Spiegelarretierung aus.
Deshalb neige ich dazu, einen größeren IE zu tolerieren.
Das gilt in besonderem Maße für Kunststoff-Sextanten.
Eine Anleitung zur Justierung der Spiegel gibt das Handbuch zum Sextanten.
- Pflege, Reinigung des Sextanten
Reinigen mit einem weichen Fensterleder. Mit Süßwasser leicht anfeuchten, mit trockener Ecke trocknen.
Fingerabdrücke: Leder mit Spiritus anfeuchten.
Zahnkranz des Limbus mit Bürste reinigen (Lieferumfang).
Nicht fetten! Fett gefährdet die Messgenauigkeit.
- Funktionsweise
Wir setzen die Gradzahl auf 0°. Mit Hilfe einer Sperrklinke kann der Zeigerarm arretiert werden.
(Bei meinem Sextanten, s. oben, ist es ein drehbarer Knopf unterhalb des Sichtfeldes)
Auch die Minutenskala stellen wir auf 0,0´; d. h. der Null-Strich der drehbaren Minuten-Skala muss exakt mit dem Nullstrich
der (festen) Nonius-Skala fluchten.
Der Sextant zeigt nun 0° 0,0´.
Nun richten wir wie der Navigator oben den Blick durch das Teleskop auf den Horizont.
Man sieht durch die Fensterglas-Hälfte des Horizontspiegels den Horizont zur Hälfte.
Die andere Hälfte wird ergänzt durch die Reflexion des oberen, schräg gestellten Indexspiegels, der (bei 0°) ebenfalls auf den Horizont
ausgerichtet ist.
Ergebnis: Wir sehen eine durchgehende Horizontlinie,
denn der eingespiegelte Horizont setzt den tatsächlich gesehenen Horizont (scheinbar) nahtlos fort.
Wenn der Zeigerarm nicht bei 0° stehen würde, sondern z. B. bei 60 °,
würde ein Objekt eingespiegelt, das sich dort (60° über dem Horizont) befindet, z. B. die Sonne.
Dann würden wir links den Horizont und rechts die eingespiegelte Sonne wahrnehmen.
- - - - -
2.3 Messen einer Gestirnshöhe (z. B. Sonnenunterrand)
Vorgang
- Fernrohr auf das eigen Auge scharf stellen.
Dazu den Indexspiegel mit allen Schattengläsern abdunkeln und nur mit dem Horizontspiegel ein entferntes Objekt anvisieren.
Solange an dern Trommel des Teleskops drehen, bis das Bild scharf ist.
- IE ermitteln (s. oben: Messfehler-Berichtigung)
- Wenigstens 1 Schattenglas, besser 2 vor den (Index-)Spiegel.
- Alhidade auf 0,0 o.
- Den Horizont möglichst genau senkrecht unter der Sonne ins Visier nehmen.
- Die Sperrklinke lösen und die Alhidade mit dem Index-Spiegel langsam nach vorne bewegen,
bis die Sonne (in der dunklen Hälfte des Sichtfeldes) auftaucht.
- Gestirn grob auf die Kimm herunterholen.
Das Gestirn bleibt ständig sichtbar, bis es die Kimm erreicht.
Sperrklinke einrasten.
- Mit der Mikrometerschraube nachjustieren.
- Exakte Messung
Rand des Gestirns exakt auf die Kimmlinie bringen.
Dabei "Pendeln": Sextant drehend hin und her bewegen.
Das Gestirn beschreibt dabei im Sextanten einen Kreisbogen.
Der tiefste Punkt des Kreisbogens soll gerade eben die Kimmlinie berühren.
- Uhrzeit festhalten, sekundengenau. (Partner!)
- Die "Sextanthöhe" ablesen (Sextantablesung, unberichtigte Höhe).
- IE und weitere Korrekturwerte (Gesamtbeschickung) anbringen.
- Positionsberechnung
Wikipedia
Messung des Sonnenunterrandes
Wikipedia: Sextant / Animation – Funktionsweise eines Sextanten . Sehr anschaulich!
Auch bei
... wird der Vorgang sehr anschaulich beschrieben und auf die Schwierigkeiten hingewiesen.
- Zeitnahme in der Praxis
Das Handling ist nicht ganz einfach ist
Wenn es nicht klappen will, kann man Folgendes probieren:
Man schätzt den Winkel der Sonne über dem Horizont.
Dazu streckt man einen Arm waagrecht nach vorne, mit dem anderen bildet man einen 45° - Winkel.
Dieser 45° - Winkel dient als Anhaltspunkt für den zu schätzenden Winkel der Sonnenhöhe.
Den geschätzten Wert stellt man im Sextanten ein und richtet den Sextanten auf den Horizont unterhalb der Sonne.
Die eingespiegelte Sonne findet man, wenn man richtig geschätzt hat, etwas unter oder über dem Horizont.
An Land gibt es keinen Horizont. Deshalb muss man mit einem künstlichen Horizont arbeiten.
Ein flacher Teller mit Wasser ersetzt ein teures Zusatzgerät.
Besser ist etwas Speiseöl, weil bei einem Luftzug die Oberfläche nicht so leicht zittert.
- Man muss die Sonne bei offenem Fenster schießen, weil die Fensterscheibe den Strahlengang beeinflussen könnte.
- Der Sextant muss nach oben die Sonne "sehen" können; der Fensterrahmen darf nicht im Wege sein.
- Wenn sich die Sonne im Wasser (oder Öl) spiegelt, gibt es keinen Horizont, auf den man die Sonne setzen könnte.
Man setzt die heruntergeholte Sonne auf den Oberrand der Sonne im Wasser so als wäre diese der Horizont.
- Beim Eingeben in das Astro-Programm von uns (s. unten) wird die Augeshöhe über dem Horizont (= Wasserspiegel, Ah) verlangt.
Bei einem künstlichen Horizont beträgt sie 0 m, wenn man dicht am Teller misst.
Zu diesem Zweck sollte man sich setzen oder den Teller z. B. auf einen Bücherstapel positionieren.
- Bei einem künstlichen Horizont verdoppelt sich der Messwinkel durch die Spiegelung.
Deshalb müssen die Ergebnisse halbiert werden.
(Umgekehrt muss die geschätzte Höhe der Sonne bei Verwendung eines künstlichen Horizontes für eine Voreinstellung verdoppelt werden.)
- Die Genauigkeit der Uhrzeit von Handy oder PC sollte überprüft werden.
Das kann man am einfachsten mit dem Zeitsignal des Fernsehers.
- Die Uhrzeit ist in UTC umzurechnen.
Wenn zwei Personen zusammenarbeiten, ruft jener mit dem Sextanten im Moment der Horizontberührung: "Jetzt!" Der Partner an der Uhr notiert die Zeit der Messung, sekundengenau.Wenn man allein ist, wird es schwieriger: Gut funktioniert es mit einer zusätzlichen Stoppuhr. Empfehlenswert ist, vor der Messung zu einer vollen Minute "einzustoppen". Uhrzeit notieren! Im Moment der Sextantmessung (Horizontberührung) hält man die Stoppuhr an. Die Zeit auf der Stoppuhr plus die notierte Einstoppzeit ergibt die Zeit der Messung.Eine gute Einführung gibt Wikipedia: https://de.wikipedia.org/wiki/Astronomische_Navigation
Umrechnung MEZ in UTC
Früher sprach man von "Greenwicher Zeit" (GMT), weil der Null-Meridian durch Greenwich verläuft.
Heute heißt sie UTC (Universal Time Coordinated).
In Deutschland gilt nicht UTC sondern Mitteleuropäische Zeit (MEZ).
Die Uhren sind bei uns um 1 h weiter als in Greenwich. Wenn es in Greenwich 12.00 ist, ist es bei uns bereits 13.00 Uhr.
Um unsere Zeit in UTC auszudrücken, muss also 1 h abgezogen werden.
Als Formel: MEZ – 1 = UTC
Für die Sommerzeit (MESZ) gilt:
MESZ – 2 = UTC
Kostenloser Download
Nun können Sie die Messergebnisse in ein Astro-Programm eingeben.
Dazu stellen wir einen Download kostenlos zur Verfügung bei:
Dort finden Sie weitere Hinweise zur Handhabung des Programms.
Ein Praktiker kann nun loslegen.
Ob die gefundene Position identisch ist mit Ihrer tatsächlichen Position, zeigen die Gradangaben bei Google Maps.
- - - - -
2.4 Beschickungen (Korrekturen), wenn man nicht mit einem Astroprogramm arbeitet.
Es gibt eine ganze Reihe physikalischer Einflüsse, die bei den Berechnungen beachtet werden müssen.
Höhe über dem wahren Horizont
Knopp: Der ... Kimmabstand Ka ist die Sextantablesung, korrigiert mit der Indexberichtigung.
Aber:
Der ... Kimmabstand eines Gestirns über der Kimm ist noch nicht die für die Rechnung benötigte Höhe über dem wahren Horizont.
Um letztere zu erhalten, müssen eine Reihe von Korrekturen angebracht werden.
Diese sind im Nautischen Jahrbuch ... zu einer Gesamtbeschickung (GB) zusammengefasst ...
Es handelt sich um folgende Einzelbeschickungen:
- Halbmesser von Sonne und Mond
- Kimmtiefe
- Strahlenbrechung
- Parallaxe
Wikipedia
Der mit dem Sextanten gemessene Winkelabstand h zwischen dem sichtbaren Horizont (der sogenannten Kimm) und dem Gestirn
muss mehrfach korrigiert werden, bevor er zur Berechnung der Position benutzt werden kann:
- Bei der Beobachtung von Sonne und Mond muss noch der halbe Durchmesser des Gestirns hinzugefügt oder abgezogen werden,
je nachdem ob man die Unter- oder Oberkante beobachtet hat.
Anm.:
Die Höhe eines Gestirns ist auf den Gestirnsmittelpunkt bezogen.
Der Radius der Scheibe von Sonne und Mond ist wegen wechselnder Erdentfernung veränderlich.
- Die Höhe des Beobachters über dem Meeresspiegel, die sogenannten Augeshöhe – sie macht die Kimm überhaupt erst sichtbar –
lässt einen zu großen Winkel messen (die Kimmtiefe).
Anm.: Die Höhe des Beobachter-Auges (Ah) verändert die Kimmentfernung.
Ah 1 m 2 3 4 5
Kimmentfernung 2 sm 3 3,5 4 4,5
- Die Lichtstrahlen der Gestirne werden in der Atmosphäre gebrochen. Diesen Effekt nennt man Refraktion ...
und er ist umso stärker, je tiefer das Gestirn steht (je näher an der Kimm).
Wenn die Sonne scheinbar untergeht, ist sie in Wahrheit schon etwa 0,6° tiefer.
Die Refraktion nimmt für kleine Winkel stark zu (bei 5 Grad rund 10') und hängt von Lufttemperatur und -druck ab.
Deshalb vertraut der Navigator einer Messung bei Kimmabstand unter 10 Grad nur eingeschränkt.
- Die Formel ζ = 90° − h (Anm.: ZD = 90 - h) gilt nur für unendlich weit entfernte Objekte.
Der dadurch verursachte Fehler heißt Horizontalparallaxe.
Sie ist bei der Astronavigation mit Sonne und Fixsternen vernachlässigbar,
aber nicht für die Planeten (Korrekturen bis etwa 0,5′) und vor allem nicht beim Mond (bis zu 1° 02′).
Werte für diese Korrekturen finden sich ... als Tabellen im nautischen Almanach ...
Wiederholung:
Die Einzelbeschickungen sind im Nautischen Jahrbuch ... zu einer Gesamtbeschickung (GB) zusammengefasst.
Bobby Schenk vereinfacht die Gesamtbeschickung des NJ noch einmal (bei 2 m üblicher Augeshöhe auf Yachten):
GB Sonnenunterrand gemessener Winkel Gesamtberichtigung
ab 20 o + 11`
ab 25 o + 12`
ab 40 o + 13`
Mit diesen wenigen Zahlen lässt sich eine Höhenwinkelmessung der Sonne ausreichend berichtigen.
Zusammenfassung
Sextantablesung + Indexbeschickung (IB) + Gesamtbeschickung (GB) = Wahre Höhe (True Alt)
Vergleich
Bsp.: Sextantablesung: 60o 45,3`, Ah 2 m, IE – 1,5 `
Gesucht: Wahre Höhe ?
Sextant: 60o 45,3`
IB + 1,5
Kimmabstand 60o 46,8`
GB nach NJ GB nach Schenk
GB (60 Grad, 2 m Ah) + 15,5 (60o 46,8`)
Zus.beschickung für Juni - 0,2 + 13`
60o 62,1`
60 ` = 1o + 1 - 60
Wahre Höhe (True Alt) 61o 02,1` 60o 59,8`
Das Ergebnis bei Schenk ist in diesem Falle um ~ 2` ungenauer. 1` entspricht 1 sm.
Schenk argumentiert, dass auf einem schwankendem Schiff die Fehler beim Messen deutlich größer sind
und das Wohlbefinden des Skippers (Seekrankheit) wichtiger als ein scheinbar exaktes Ergebnis.
- - - - -
2.5 Künstlicher Horizont
Er wäre nötig, um nachts zu messen.
Es gibt entsprechende Vorrichtungen (Libelle) bei hochwertigen (teuren) Sextanten als Zusatzausstattung.
Damit aber sprengt es meinen Ansatz der "Einfachheit", was durchaus gleichbedeutend ist mit "nicht zu teuer".
Preiswert ist ein Teller mit Wasser (s. weiter unten).
Wikipedia:
Ein künstlicher Horizont … ersetzt den natürlichen Horizont, der die Grenzlinie zwischen der sichtbaren Erde
und dem Himmel darstellt, wenn man den Horizont nicht sehen kann …
Bei schlechten Sichtbedingungen oder bei Beobachtungen auf dem Lande, wenn die Sicht auf die Kimm durch Häuser,
Berge oder Vegetation versperrt ist, braucht man einen künstlichen Horizont in Gestalt einer exakt horizontal liegenden,
spiegelnden Fläche (Quecksilber oder schwarz gefärbte, polierte Glasplatte oder Öl),
die als Hilfsmittel zur Darstellung der Lotrichtung dient.
Die Glasplatte (der künstliche Horizont) ruht in einer Metallfassung und wird durch drei Stellschrauben
unter Verwendung von zwei Setzlibellen horizontiert.
Bei der Höhenmessung geht es darum, das betreffende Objekt mit dessen Spiegelbild zur Deckung zu bringen.
Dabei entspricht der Winkel zwischen dem direkten und dem am künstlichen Horizont reflektierten Strahl der doppelten Höhe,
ist also zu halbieren. …
2.6 Teller mit Wasser als künstlicher Horizont (auch mit Speise-Öl)
Zum Üben kann man selbst einen einfachen, künstlichen Horizont herstellen: einen Teller (oderr ein Backblech) mit Wasser (oder Öl).
Prinzip:
- Man bringt das Gestirn mit seinem Spiegelbild zur Deckung und erhält dadurch die doppelte scheinbare Höhe.
Deshalb muss der Messwert halbiert werden.
Für die Berechnung: IB anbringen, berichtigten Messwert halbieren.
Gerechnet wird vom Mittelpunkt des Gestirns zum Horizont, oder - in unserem Fall - zum Mittelpunkt der gespiegelten Sonne.
Deshalb muss der Radius der Sonne weder abgezogen noch addiert werden.
In der Gesamtbeschickungstafel ist aber genau dies eingerechnet. Deshalb kann man diese Tafel nicht benutzen,
sondern muss sich die fehlenden Korrekturen zusammensuchen. Das macht es kompliziert.
Fehlende Einzelkorrekturen: Kimmtiefe, Strahlenbrechung, Parallaxe
Einfacher ist das folgende Verfahren:
- Man bringt die heruntergezogene Sonne mit dem Spiegelbild im Wasser nicht zur Deckung, sondern setzt sie auf die "untere" Sonne auf,
wie auf den Horizont.
Vom Mittelpunkt der unteren Sonne zum Mittelpunkt der oberen Sonne sind 2 r (der Sonne).
Durch die Halbierung des Messwerts wird ein r herausgerechnet, das zweite r wird in der Gesamtbeschickungstafel berücksichtigt.
Berechnung: IB anbringen - berichtigten Messwert halbieren - GB.
Diese Methode hat zusätzlich den Vorteil, dass durch das Aufeinandersetzen des scharf zu sehenden Sonnenunterrandes
auf den Sonnenoberrand der "unteren" Sonne die Messung genauer wird.
Praxis
- Man suche sich eine windgeschützte, sonnenbeschienene Stelle im Haus.
- Wenn es sich um ein Fenster handelt, muss das Fenster geöffnet werden.
Denn der Brechungsindex von Glas verfälscht die Messungen.
Eine geöffnete Tür im Raum verursacht meist einen Zug (Luftströmung). Türe schließen.
- Der Sextant muss die Sonne "sehen" können, darf also nicht beschattet sein.
- Möglichst großenTeller mit Wasser vor sich aufbauen, evtl. auf einem Tischchen, der Fensterbank etc.
- Man sollte möglichst nahe an den Teller mit Wasser heranrücken.
- Schattengläser! Wenigstens eins, vor den Horizontspiegel und ebenso vor den Indexspiegel.
- Sonne herunterholen
- Es ist nicht ganz einfach die Sonne im Index-Spiegel zu finden.
Wenn die Methode des normalen "Herunterholens" im Wasserspiegel (s. oben) nicht funktioniert will, geht vielleicht folgender Weg:
Kein Schattenglas vor den Horizontspiegel. Alhidade auf 0 o .
Einen Ersatz-Horizont (z. B. Hausfirst) möglichst genau senkrecht unter der Sonne anvisieren.
Die Alhidade nach vorne bewegen, bis die gespiegelte Sonne auftaucht.
Herunterholen der Sonne auf den Ersatzhorizont (s. oben: "Messen einer Gestirnshöhe").
Winkel ablesen. Winkel verdoppeln!
Schattenglas vor den Horizontspiegel.
Sextant auf die Sonne im künstlichen Horizont (Wasser im Teller) richten.
Im Sextant müsste die "Indexspiegel-Sonne" neben der "Horizont-Sonne" wenigstens auftauchen.
Jedenfalls befindet sie sich im "Nahbereich".
In jedem Falle wird man den Sextanten etwas pendeln müssen, damit das Gestirn entdeckt werden kann.
Dann Feinjustierung.
- Gesamtbeschickung (GB) mit Augenhöhe 0 m, denn man befindet sich ja unmittelbar am Wasserspiegel (= Horizont).
- - - - -
2.7 Stellarium
Wikipedia:
Funktionen
wobei Ort und Zeit sowie der Raumwinkel frei gewählt werden können. …
Stellarium ist ein gigantisches Programm.
Es kann kostenlos heruntergeladen werden, z. B. bei chip.de
Für uns ist es als Kontrollinstrument sehr nützlich.
Wenn man die Sonne als Gestirn einstellt, den eigenen Ort, das Datum und die genaue Uhrzeit, kann man z. B. die genaue Sextanthöhe ablesen.
In der Praxis kann ich überprüfen, ob meine Messung richtig ist bzw. um wieviel sie vom richtigen Wert abweicht.
Es ist nicht ganz einfach, aus der Fülle der Möglichkeiten die richtigen anzuklicken.
Einstellungen
Die Eingangsfenster befinden sich am linken und am unteren Rand des Bildschirms.
Der Zeiger muss an den Rand geführt werden und zwar in Höhe der Symbole:
linker Rand - untere Hälfte, unterer Rand – linke Hälfte.
Wenn man den Zeiger auf einem Symbol ruhen lässt, erscheint seine Bedeutung als Schrift.
Linker Rand, von oben nach unten
Symbol
- Standortfenster achteckiger Stern mit Achse oder Zentrum
- Datum- und Zeitfenster Haken im Kreis
- Himmel- und Anzeigenoptionsfenster weißes Feld mit Stern, Saturn und Spiralnebel
- Suchfeld Lupe mit Stern
- Einstellungsfenster Werkzeugschlüssel mit Stern
Wenn man Stellarium öffnet und der Bildschirm ist schwarz, heißt das, man hat die Nacht erwischt.
- Deshalb zunächst im Datum- und Uhrzeitfenster die Uhrzeit so ändern, dass es hell wird.
Die Uhr läuft (in UTC) weiter.
Am unteren Bildrand findet man das Dreieck, das man von Youtube her kennt. Anklicken!
Dann erscheinen die beiden bekannten Balken und die Zeit steht.
- Standortfenster:
Es sind unzählig viele Standorte zum Anklicken vorbereitet.
Wenn der eigene Standort nicht dabei ist, kann man ihn eingeben mit Name und den Koordinaten,
die man entweder vom Handy oder von Google Maps erhält. Abspeichern!
- Himmel- und Anzeigeoptionsfenster: Projektion / Perspektiven anklicken
- Suchfeld: Sonne anklicken
- Einstellungsfenster: rechts oben Erweiterungen anklicken, dann Navigationssterne
Unterer Rand, von links nach rechts.
Wenn man den Zeiger auf den Symbolen ruhen lässt, erscheint ganz links die Bedeutung.
Die für uns wichtigen sind:
Symbol
- Boden kleiner und großer Kugelbaum
- Atmosphäre Sonne hinter Gebüsch
- Himmelsrichtungen 4-zackige Kompassrose
- Vollbildmodus 4 Pfeile von einem Mittelpunkt ausgehend
- Typischer Stern für Astronavigation Sextant
- Zeitablauf Dreieck als Startsymbol und Doppelbalken
- Aktuelle Zeit verwenden Sanduhr
- Beenden das übliche Beenden-Zeichen
Sonnenhöhe ablesen
Wie hoch steht die Sonne
in Röthenbach an der Pegnitz (49° 48,4´; 11° 24,3´)
am 20. Nov. 2023
um 10 Uhr 30 Min. 0 Sek. ?
Das muss eingestellt und angeklickt werden:
Linker Rand
- Standortfenster: Roethenbach, Westeuropa
- Datum-, Uhrzeitfenster 2023 – 11 – 23; 10 : 30 : 00
Uhr anhalten: am unteren Rand …
- Einstellungsfenster Erweiterungen / Navigationssterne
- Suchfeld: Sonne
Unterer Rand
- Symbol: Sextant
- Zeitablauf: Doppelbalken, damit die Uhr stehen bleibt.
Am linken Rand (Zeiger an den Rand) erscheint eine Liste von Daten, die sich auf die Sonne beziehen (Überschrift Sonne).
Etwas über der Mitte findet man den Wert für Ho .
In diesem Fall: Ho 20° 14,8´
- - - - -
2.8 Begriffe
Nautisches Jahrbuch (NJ)
Wikipedia (2010):
Das Nautische Jahrbuch ist das amtliche Handbuch für die astronomische Navigation in der deutschen Hochseeschifffahrt.
Das Jahrbuch enthält die Ephemeriden von Sonne, Mond, den vier Navigationsplaneten (Venus, Mars, Jupiter und Saturn),
des Frühlingspunktes sowie die festen Koordinaten der Navigationssterne für jeden Tag eines Jahres in einstündigem Abstand
für Universal Time No.1 (UT1) …
Unter Verwendung eines Sextanten und einer genau gehenden Uhr
lässt sich aus diesen Daten die astronomische Ortsbestimmung durchführen….
Das NJ war in jeder Buchhandlung erhältlich.
2020 wurde vom BSH (Bundesamt für Seeschifffahrt und Hydrographie) das letzte amtliche Nautische Jahrbuch verlegt.
Jetzt (2023) liegt ein neues, von Harald Merkel privat ediertes Nautisches Jahrbuch vor (Independentley Published).
Das Nautische Jahrbuch 2023 wird von einem privaten Verleger herausgegeben.
Es ist im Layout stark an die Version vom BSH angelehnt und daher damit vergleichbar.
Meines Wissens sind auch die enthaltenen Informationen vergleichbar.
Im Vertrauen auf diese Auskunft, verändere ich meine Hinweise zum NJ nicht.
Ephemeriden Wikipedia: Die Ephemeriden … sind die Positionswerte sich bewegender astronomischer Objekte
bezogen auf ein ... astronomisches Koordinatensystem.
Nautical Almanach Englisches Pendant zum Nautischen Jahrbuch
Augeshöhe (Ah) Die Höhe des beobachtenden Auges über dem Wasserspiegel. (Claviez)
Die Bezugsebene in der Astronavigation ist der Meeresspiegel.
Der Messpunkt , die Augeshöhe, kann in ihrer Höhe erheblich davon abweichen, z. B. h und H in der folgenden Skizze,
wenn dort gemessen würde:
(Wikipedia)
Kimm Auf freier See die Linie, in der Himmel und Erde sich zu berühren scheinen, der sichtbare Horizont.
Die Entfernung der Kimm vom Beobachter ist abhängig von dessen Augeshöhe
und beträgt mit großer Annäherung e = 2,075 * Wurzel Ah (Claviez)
Kimmtiefe (Depression; depression of the horizon; dip of the horizon, Dip)
Der Winkel, um den am Auge des Beobachters die Kimm unter dem scheinbaren Horizont liegt,
der Winkel, den die Tangente an die Meeresoberfläche mit der Horizontalen bildet.
Dieser Winkel ist abhängig von der Augeshöhe des Beobachters und atmosphärisch bedingter Strahlenbrechung. (Claviez)
Sextantablesung (Alt Sext) der Wert, den der Sextant zeigt, ohne Korrektur
Indexfehler (Index-Error; IE) Fehler bei der Messung; zeigt die Trommel z. B. 58`, dann ist der IE – 2,
die Indexberichtigung (IB) + 2.
Indexberichtigung (-beschickung; IB) s. Indexfehler
wahrer Horizont Der mit dem Sextanten gemessene Kimmabstand ... ist noch nicht die für die Rechnung benötigte Höhe
über dem wahren Horizont.
Um letztere zu erhalten, müssen eine Reihe von Korrekturen angebracht werden. (Knopp)
Nämlich die Beschickungen (s. Gesamtbeschickung).
Kimmabstand (Ka) Sextantablesung korrigiert mit der Indexberichtigung (Knopp)
Beschickung Berichtigung, Korrektur; im engeren Sinne die physikalischen Korrekturwerte einer Gestirnsmessung,
nicht die Korrekturen am Sextanten.
Gesamtbeschickung (GB) alle physikalisch notwendigen Berichtigungen einer Gestirnsmessung
zusammengefasst in einem Tafelwert (s. Kimmabstand)
wahre Höhe, Höhenwinkel, Höhe (h) auch (ho True Alt)
Der Winkel, der vom Standort des Beobachters zwischen Gestirn und Horizont im Sextanten gemessen wird
nach Indexberichtigung (IB) und Gesamtbeschickung (GB).
Sextantablesung + IB + GB = wahre Höhe
- - - - -
Literatur
Knopp, Helmut Astronomische Navigation, 1986
Blewitt, Mary Navigieren nach Gestirnen, 1975
Claviez, Wolfram Seemännisches Wörterbuch, 1973
- - - - -
2. NordsternbreiteWie findet man den Polarstern?Wenn man die Hinterachse des Großen Wagens (auch: Großer Bär) 5 x verlängert, stößt man auf den Polarstern.Er ist gleichzeitig der Deichselstern des Kleinen Wagens (Kleiner Bär).
Wikipedia: 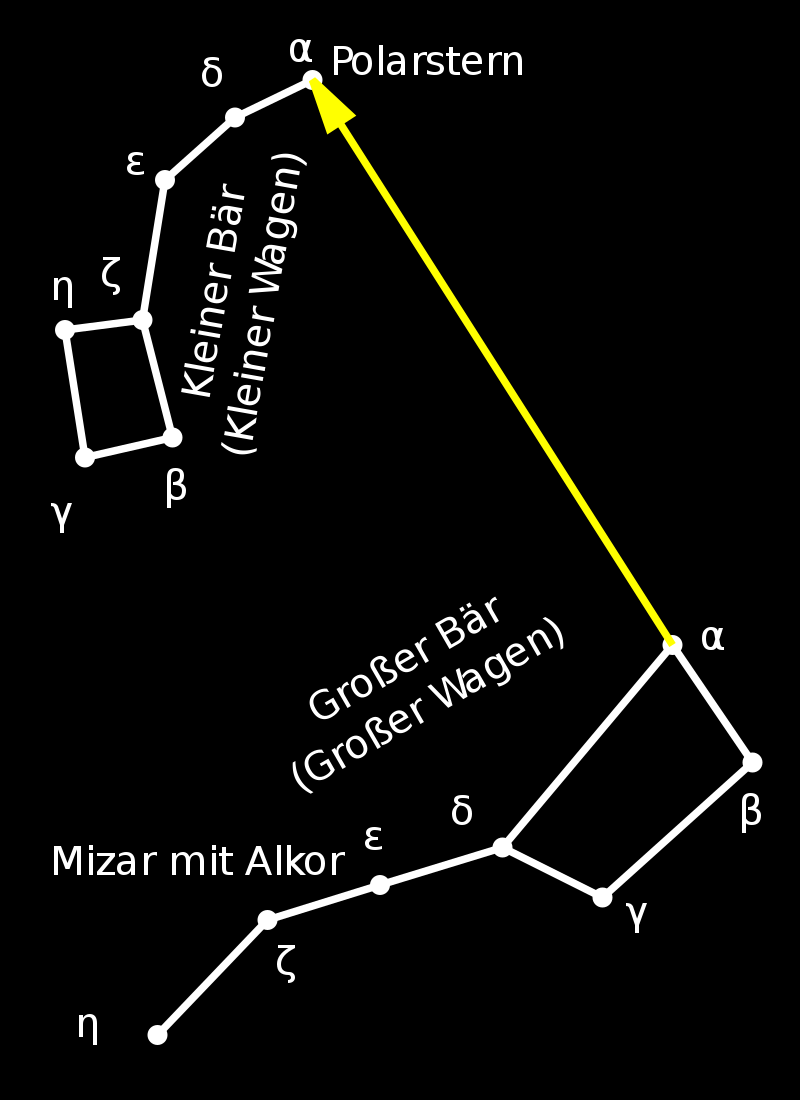
Nordsternbreite
Das Verfahren ist sehr anschaulich geschildert bei
https://yachtschule-dreyer.de/images/sampledata/asimages/kurse/Astrokurs.pdf
Die Messung des Nordsterns mit dem Sextanten ergibt unmittelbar die Breite des Beobachters.
- Sextantmessungen
Wikipedia skizziert das grundsätzliche Verfahren, das für alle Sextant-Messungen gilt:
(Wikipedia)
Die Sonne ist so weit entfernt, dass ihre Strahlen quasi parallel in Z und O (dem Standort des Beobachters) auftreffen.
Der Beobachter misst mit dem Sextanten den Winkel zwischen Horizont und z. B. dem Unterrand der Sonne, die Sonnenhöhe (h).
Zenit und Horizont stehen im 90°-Winkel zueinander.
In der Skizze ist nicht der Winkel h sondern der Komplementärwinkel 90° - h rot eingezeichnet. (Dieser Winkel heißt Zenitdistanz, ZD).
Höhe + Zenitdistanz ergeben immer 90°: h + ZD = 90°
Der Ort, in dem die Sonne im Zenit steht, ihr Bildpunkt, ist mit Z markiert.
Zur besseren Deutlichkeit sollte man auf die Originalseite von Wikipedia gehen und die Vergrößerung anklicken.
Nun soll nicht die Sonne gemessen werden sondern der Nordstern (Polarstern).
An die Stelle der Sonne (in der obigen Skizze) tritt der Nordstern.
Der Nordstern steht genau über dem Nordpol. Immer!
Am nächtlichen Himmel kreisen die Sterne um ihn, er ruht.
Z in der obigen Skizze wird damit zum Nordpol.
Von der Skizze in Wikipedia zu meiner Skizze:
Wichtig für das Verständnis ist wiederum, dass die Lichtstrahlen eines Gestirns parallel auf die Erde auftreffen.
Gemessen wird mit dem Sextanten die Nordsternhöhe h.
Die Zenitdistanz ZD errechnet sich aus 90 – h.
Auf der Erdoberfläche ist der Abstand vom Äquator zu den Polen jeweils in 90 Breitenkreise aufgeteilt.
I) Auf welchem Breitengrad man auch den Nordstern misst, immer ergeben der gemessene Winkel h (Höhe) plus die davon abhängige Zenitdistanz (ZD) 90 Grad.
h + ZD = 90
h = 90 - ZD
II) Der Winkel ZD wiederholt sich am Erdmittelpunkt (Wechselwinkel an Parallelen).
Auch hier liegt ein rechter Winkel vor.
ZD + 𝜑 = 90
𝜑 = 90 - ZD
III) I und II lassen sich also gleichsetzen:
h = 𝜑
In Worten:
Der gemessene Winkel entspricht dem Breitengrad des Beobachters.
Mathematischer fomuliert:
Die Polhöhe ist gleich der geographischen Breite des Beobachters.
Es gibt zwei Probleme:
- Der Nordstern steht nicht exakt über dem Nordpol.
Er ist etwa um 1° davon entfernt.
Berichtigungstabellen findet man aber im Nautischen Jahrbuch. Dieses Problem ist demnach lösbar.
- Das größere Manko: In der Dämmerung ist der Nordstern kaum sichtbar.
Und nachts ist der Horizont nicht erkennbar. Auch nicht bei Vollmond.
Daher kann man nachts bestenfalls annäherungsweise Sextant-Messungen vornehmen.
Es sei denn, man verwendet einen "Künstlichen Horizont".
- - - - -
Begriffe
Verwirrend! Denn es gibt deutsche, englische, lateinische und griechische Fachbegriffe und dazu die jeweiligen Abkürzungen.
Die folgenden Definitionen aus Wikipedia
1 Breitenkreise
In der folgenden Skizze wird deutlich, dass sowohl die Breite φ (auch Φ = Phi; engl. Latitude, Lat.)
als auch die Länge λ (= Lambda) Winkel sind, die vom Erdmittelpunkt aus gemessen werden.
(Wikipedia)
Der Abstand zwischen zwei Breitenkreisen beträgt 1°.
Bei 40.000 km Erdumfang ist 1° (40.000 : 360 ) 111,11 km
1´ (111,11 : 60) 1,852 km = 1 sm
60 ´ sind 1 °, und damit 1° = 60 sm
Für die Längenkreise (Meridiane) gilt diese Rechnung nur am Äquator. Zu den Polen hin verkürzen sich deren Abstände.
- Höhe, Höhenwinkel (h; Altitute, ALT)
So heißt der mit dem Sextanten gemessene Winkel zwischen Horizont und Gestirn.
- Zenit (Z)
Der Zenit ist die nach oben verlängerte Lotrichtung eines Standortes.
Zenitdistanz (ZD, Zenitwinkel, z; auch Phi, φ)
Der Zenit steht im 90o - Winkel zum Horizont.
Bei einer Gestirnsmessung wird der Winkel Horizont – Gestirn gemessen.
Der Winkel zwischen Höhenwinkel und Zenit heißt Zenitdistanz.
Blewitt: Die Zenitdistanz (ZD) ist der Komplementärwinkel der Höhe.
Höhe plus Zenitdistanz ergeben immer 90 o.
H plus ZD = 90
- Bildpunkt (BP, engl: Geographical Position, GP)
… ist der Punkt, an dem eine gedachte Linie vom Mittelpunkt der Sonne zum Mittelpunkt der Erde die Erdoberfläche durchdringt.
Für einen Beobachter, der auf der Erdoberfläche im Bildpunkt der Sonne steht, befindet sie sich im Zenit.
(Die Definitionen gelten für alle Gestirne. Ich beschränke mich in allen Beiträgen auf die Sonne.)
- Deklination der Sonne (δ = Delta; Dek., engl. Declination, Dec.)
… ist die geographische Breite, auf der ihr Bildpunkt dahinrast.
Die Sonne bewegt sich im Jahresverlauf zwischen den Wendekreisen N, dem Wendekreis des Krebses (+ 23,43472°),
und S, dem Wendekreis des Steinbocks (- 23,43472°), hin und zurück.
Am Tag der Sommersonnenwende (21. Juni) steht sie am weitesten nördlich, am Tag der Wintersonnenwende (21. Dez.) am weitesten südlich.
Wenn die Sonne den Äquator überquert - zur Zeit der Tag- und Nachtgleiche - ist ihre Deklination 0 °.
(Wikipedia)
Die Deklination der Sonne verändert sich im Verlauf des Jahres alle vier Tage nur um durchschnittlich 1°.
Aber das Tempo der Änderung schwankt: an den Tagen der Sommer- und Wintersonnenwende sind es jeweils 0,1´,
an den Tagen von Tag- und Nachtgleiche (21. 3. und 21. 9.) sind es 23,7´.
Die Deklination der Sonne ist im Nautischen Jahrbuch aufgelistet.
(Auch die Länge, der sog. Greenwicher Stundenwinkel. Darüber später.)
Nautisches Jahrbuch (NJ)
Das Nautische Jahrbuch war das amtliche Handbuch für die astronomische Navigation.
Es enthielt die Ephemeriden (= Positionen) von Sonne, Mond und ausgewählten Sternen für jeden Tag eines Jahres
in einstündigem Abstand (Zwischenwerte konnten interpoliert werden) und zusätzlich eine Reihe von Tafelwerken.
2020 wurde das letzte amtliche Nautische Jahrbuch vom Bundesamt für Seeschifffahrt und Hydrographie (BSH) verlegt.
Seit 2023 wird es wieder privat ediert.
- - - - -
4. Mittagsbreite (Mittagshöhe)
Wenn die Sonne kulminiert, steht sie auf der Nordhalbkugel der Erde genau im Süden des Beobachters.
In dieser speziellen Situation lässt sich die Breite der Beobachterposition leicht ermitteln:
- Man misst mit dem Sextant den Winkel zwischen Horizont und Unterrand des Gestirns zum Zeitpunkt der Kulmination (Höchstand),
- berichtigt diesen Wert um die notwendigen Korrekturen,
- schlägt die Deklination der Sonne (= "Breite" ihres Bildpunktes; s. Begriffe) im aktuellen Nautischen Jahrbuch (NJ) nach
- und berechnet nach einer einfachen Plus-/Minus-Formel den Breitengrad, auf dem sich die Yacht befindet.
Wann ist Schiffsmittag?
Dann, wenn die Sonne am Schiffsort kulminiert, also den höchsten Punkt der Sonnenbahn durchläuft.
Bekannt ist, wo sich das Schiff etwa befindet. Angenommen etwa am 35. Längengrad W, 10. November (2010).
Die Sonne kulminiert, wenn sich ihr Bildpunkt auf dem gleichen Meridian wie das Schiff befindet.
Die Länge des Sonnenbildpunktes wird im NJ mit Grt (Greenwicher Stundenwinkel) angegeben.
Man schlägt den 10. Nov. auf und sucht den Grt der Sonne, der möglichst nahe an 35o herankommt.
Im Nautischen Jahrbuch steht für diesen Tag:
UTC 14.00 / Grt 034o 01,0´
UTC 15.00 / Grt 049o 01,0´.
Die Sonne wird also zwischen 14 und 15 Uhr Weltzeit kulminieren, eigentlich unmittelbar nach 14.00 UTC.
Das würde für die Praxis genügen.
Es lässt sich genau berechnen:
Wie lange braucht die Sonne von 34o 01,0´ nach 35o 00,0´?
35o 00,0` = 34o 60,0 ´
- 34 01,0
59,0 ´
Für 360 o braucht sie 24 h. Für 1 o also ... ?
Zuerst müssen die Stunden in Minuten umgerechnet werden: 24 h * 60 = 1440 min.
1440 min : 360 = 4 min
Die Sonne benötigt demnach 4 Min. für einen Längengrad (= 60´). Für 59´ noch etwas weniger.
4 min sind 240 sec.
Für 1 Längen-Minute also 240 : 60 = 4 sec.
Für 59,0 ´ braucht die Sonne 4 * 59 = 236 sec. = 3 min 56 sec
Um 14.00 UTC kulminiert die Sonne auf dem Meridian Grt 34o 01.0´.
Wenn unser Schiff wirklich auf 35o stehen würde, würde die Sonne um 14 h 03 min 56 sec UTC kulminieren.
Mit Hilfe des Nautischen Jahrbuchs ließe sich die obige Rechnung umgehen:
Es gibt die sog. Schalttafel (blaue Seiten), in der die Umrechnungen aufgelistet sind.
Beim "Zuwachs Grt" für die Sonne findet man unter 0o 59,0` 3 min 56 sec.
Messung in der Praxis
Etwa eine halbe Stunde vor dem geschätzten Schiffsmittag (Kulmination der Sonne, Meridiandurchgang) würde man sich
mit dem Sextanten an Deck begeben.
Wenn man die Sonne auf den Horizont herunterholt und nach kurzer Zeit wieder durch den Sexanten sieht, stellt man fest,
dass die Sonne nach oben wandert. Sie ist also auf dem Weg zum Kulminationspunkt.
Sie steigt zunächst relativ rasch.
Wenn sie sich dem Scheitel nähert, verflacht die Tagbogen-Kurve der Sonne; sie ändert die Höhe kaum mehr.
In dieser Phase muss man ständig die Sonne durch den Sextanten betrachten und sie solange auf den Horizont herunterholen,
also am Nonius nachdrehen, solange ihr Bild über (!) dem gespiegelten Horizont im Sextanten steht.
Ab dem Moment, wo die Sonne nicht mehr steigt, nichts mehr machen!
In dem Augenblick, in dem man den Unterrand etwas unter dem eingespiegelten Horizont im Sextanten beobachtet,
beginnt die Kurve zu fallen; die Kulmination ist vorbei.
Wenn man alles richtig gemacht hat, hat man den höchsten Winkel, den Kulminationswinkel, im Sextanten festgehalten.
Ablesen!
IB (Indexberichtigung) und GB (Gesamtbeschickung) anbringen.
Breite berechnen:
Auf der Nordhalbkugel gilt im astronomischen Sommerhalbjahr, und wenn der Bildpunkt der Sonne nicht nördlich des Beobachtungsortes liegt,
folgende Formel:
Beobachterbreite = Zenitdistanz + Deklination (des BP der Sonne)
LAT (φ) = ZD + Dec (δ)
Astronomische Zusammenhänge
Es gibt mehrere mögliche Konstellationen hinsichtlich Bildpunkt der Sonne (BP) und Beobachtungsort (O; Schiffsposition).
Fall 1:
Sowohl der Beobachtungsort als auch der Bildpunkt liegen auf der Nordhalbkugel.
Man nennt diese Konstellation "gleichnamig".
Es ist die im Sommerhalbjahr übliche Konstellation, wenn sich das Schiff auf der nördlichen Nordhalbkugel befindet.
Rechenschema:
Beobachterbreite = Zenitdistanz + Deklination
LAT (φ) = ZD + Dec (δ)
Fall 2:
Wenn der Bildpunkt der Sonne im Winterhalbjahr auf die Südhalbkugel wandert, würde man (bei gleichem Beobachtungsort)
von „ungleichnamig“ sprechen.
Verfertigen Sie eine entsprechende Skizze und entwickeln Sie die Berechnungsformel.
Sie müssten auf folgendes Schema kommen:
Beobachterbreite = Zenitdistanz - Deklination
LAT (φ) = ZD - Dec (δ)
M. Blewitt fasst beide Fälle zu einer einzigen Formel zusammen:
Fall 1 und 2:
Beobachterbreite = Zenitdistanz + gleichnamige / - ungleichnamige Deklination
LAT (φ) = ZD + gleichnamige / - ungleichnamige Dec (δ)
Fall 3
Wenn der Bildpunkt der Sonne zwischen dem Beobachter und dem oberen Pol steht, ergibt sich:
Breite = Deklination - Zenitabstand
LAT (φ) = Dec (δ) - ZD
- - - - -
Begriffe
Schiffsmittag Der Begriff hat mit dem normalen "Mittag" nichts zu tun.
Schiffsmittag ist dann, wenn die Sonne sekundengenau exakt im Süden des Beobachters steht.
s. Kulmination und Meridiandurchgang
Beobachtungsort (meist gleichzeitig Schiffsort, Position)
Er wird durch die Koordinaten ...
- Breite φ (Phi, fi) / LAT / latitude
- Länge λ (Lambda) / long / LON / longitude
... bestimmt.
Vgl. Terrestrische Navigation / Grundwissen
Zenit (Z)
Wenn eine Gerade vom Erdmittelpunkt durch deinen Standort und hinaus in den Weltraum gezogen würde,
so würde sie zu deinem Zenit führen. (Plewitt)
Einen Zenit gibt ist in jedem Punkt auf der Erde. Es ist z. B. der Punkt senkrecht über dem Beobachter,
in dem eine in gegensätzlicher Richtung zur Schwerkraft gedachten Gerade die Himmelskugel trifft.
In der folgenden Skizze von Wikipedia ist es die blaue Linie über dem Beobachtungspunkt, die zum Zenit des Beobachters weist.
Sie steht senkrecht auf der Beobachtungsebene.
Auch der Bildpunkt der Sonne hat einen Zenit ...
*: Sonne
Z: Ort, über dem die Sonne im Zenit steht
Anm.:
Z ist hier gleichzeitig der Bildpunkt der Sonne.
Deshalb sollte dieser Punkt besser oder zusätzlich mit BP (Bildpunkt) bezeichnet werden.
Für die weiteren Überlegungen ist wichtig, dass die Strahlen der Sonne quasi parallel auf die Erde treffen, weil die Sonne sehr weit entfernt ist.
Die beiden roten Linien entsprechen diesen Strahlen.
Der Beobachter würde aber nicht den angedeuteten Winkel mit dem Sextanten messen, sondern den Winkel zwischen Beobachtungsebene
(der Ebene auf der das Männchen steht, in Verlängerung) und Sonnenstrahl z. B. des Sonnenunterrandes.
Der im Bild von Wikipedia ausgewiesene Winkel φ heißt "Zenitdistanz".
Bildpunkt (BP, Geographical Position, GP)
"... der Bildpunkt (GP) der Sonne ... liegt dort,
wo die vom Erdmittelpunkt zur Sonne gezogene Gerade die Erdoberfläche schneidet. ... " (Plewitt)
"Verbindet man ... z. B. ... den Mittelpunkt der Sonne, mit dem Mittelpunkt der Erde, so trifft diese Verbindungslinie
die Erdoberfläche in einem ganz bestimmten Punkt. Dieser Punkt heißt Bildpunkt." (Knopp)
Weil die Sonne sich in 24 h um die Erde bewegt, wandert der Bildpunkt entsprechend schnell:
40.000 km : 24 h = 166 6,6 km/h : 60 = 27.77 km/min : 60 = 0.463 km/sec.
In 4 sec also 1.852 m = 1 sm.
" Nicht nur die Sonne, sondern alle anderen Gestirne haben ihre GPs, deren Lage zu jedem beliebigen Zeitpunkt
dem ... Nautischen Jahrbuch entnommen werden kann." (Plewitt)
Bestimmung des Bildpunktes (BP) durch die Koordinaten ...
- Deklination "Bildpunktbreite" = Deklination (Dec; δ); auch Abweichung
- Stundenwinkel "Bildpunktlänge" = Greenwicher Stundenwinkel (Grt, Greenwich Hour Angle, GHA)
Erläuterung später.
Zenitdistanz (z, ZD) Zenitabstand; Winkelabstand eines Gestirns vom Zenit.
Gestirnshöhe (mittels Sextanten gemessen, berichtigt) plus Zenitdistanz ergeben 90 Grad
Als Formel:
H + ZD = 90 o
ZD = 90 o – H
Deklination der Sonne (Dec / Declination / Bildpunktbreite / Abweichung, δ (Delta))
In der Astronomie bezeichnet … Deklination der Sonne … die geographische Breite, in der die Sonne im Zenit steht. …
(Plewitt)
Die Deklination der Sonne schwankt zwischn 23 o Nord in der Mitte des Sommers, wenn sie den Wendekreis des Krebses erreicht,
und 23 o S in der Mitte des Winters am Wendekreis des Steinbocks.
Im Frühjahr und im Herbst, während der Tag- und Nachtgleiche (wenn die Sonne den Äquator überquert), ist ihre Deklination 0 o.
(Wikipedia)
Deklination eines Gestirns
Die Deklination eines Gestirns ist der Breitengrad (kurz "Breite") seines GPs (Bildpunkt). (Plewitt)
Die Deklination gibt die nördliche oder südliche Breite des Bildpunktes an und ist seine Position auf der Erdoberfläche:
von 0 – 90 nach N (als " + ") und nach S (als " - ").
Die Deklination der Sonne ( δ) und der Stundenwinkel (= "Länge", Grt) sind im Nautischen Jahrbuch für jede Stunde des Jahres aufgelistet.
Aus einer Zusatztabelle ("Schalttafel") lässt sich der genaue Wert für jede Sekunde des Jahres bestimmen.
Kulmination, Meridiandurchgang
Wenn die Sonne für einen Beobachter den höchsten Punkt der Sonnenbahn erreicht hat, spricht man von der Kulmination der Sonne.
Auf Nordhalbkugel steht die Sonne in diesem Moment genau im Süden des Beobachters.
Schiff und Sonnenbildpunkt befinden sich in diesem Augenblick auf gleicher Länge, dem gleichen Meridian.
Deshalb spricht man auch vom Meridiandurchgang.
Wenn man in diesem Moment die Sonne "schießt", ergeben sich bestimmte rechnerische Zusammenhänge (s. oben).
- - - - -
III. Astronavigation für Fortgeschrittene
Wer sich ernsthaft mit Gestirnsmessungen beschäftigen will, sollte sich ein Lehrbuch zulegen.
Ich empfehle: Helmut Knopp, Astronomische Navigation
5. Umrechnung von Zeit (Zeitmaß) in Länge (Bogenmaß, Gradmaß)
Die Erde dreht sich in 24 Stunden um 360o.
In 24 h werden 360 o zurückgelegt. (= 40.000 km)
In 1 h werden (360 : 24) = 15 o zurückgelegt.
Das sind umgerechnet 60 min und (15 x 60 = ) 900 ´ (Bogenminuten) (= 1.666.66 km)
In 1 min werden (900 : 60) = 15 ´ zurückgelegt.
Das sind umgerechnet 60 sec und (15 x 60 = ) 900 ´´ (Bogensekunden) (= 27.77 km)
In 1 sec werden (900 : 60) = 15 ´´ zurückgelegt. (= 0,4629 km = ~ 463 m)
Zusammengefasst:
1 h entspricht 15 o
1 min 15 ´
1 sec 15 ´´
- Bogenmaß in Zeit
Nun in die andere Richtung:
Wie lange braucht die Sonne, um die Strecke von 1o zurückzulegen?
Dazu müssen wir die Grad in Bogenminuten umrechnen:
360 x 60 = 21600 Bogenminuten
... und die 24 h in Zeitminuten: 24 x 60 = 1440 min
Die Sonne (eigtl. ihr Bildpunkt) legt also 21600 Bogenminuten in 1440 Zeitminuten zurück.
Wieviel legt die Sonne in 1 (Zeit)-Minute zurück?
21600` : 1440 min = 15´
Die Sonne legt in 1 Min. (Zeit) 15´ (Bogenminuten) zurück.
In 4 Minuten ist das (4 x 15 =) 1o
Dieselbe Rechnung für 1 (Zeit-)Sekunde:
In 1 min legt sie 15´zurück.
Das sind 60 sec und (15 x 60 =) 900 ´´
In 1 sec legt sie (900 : 60 = ) 15 ´´ zurück.
Zusammengefasst
1o (im Bogenmaß) entsprechen 4 min (im Zeitmaß)
1´ (im Bogenmaß) 4 sec (im Zeitmaß)
Wieviel km sind 1´:
Der Erdumfang (40.000 km) geteilt durch 360 o = 1 o (= 111.11 km)
1 o durch 60 ´ = 1 ´ ( = 1.852 km = 1 sm)
- - - - -
Tabelle: Umrechnung von Zeit in Bogenmaß
Stunden = o Minuten = o + ´
1 h = 15 o 1 min = 0 o 15 ´ 31 min = 7 o 45 ´
2 30 2 0 30 32 8 00
3 45 3 0 45 33 8 15
4 60 4 0 60 34 8 30
5 75 5 1 15 35 8 45
6 90 6 1 30 36 9 00
7 105 7 1 45 37 9 15
8 120 8 2 00 38 9 30
9 135 9 2 15 39 9 45
10 150 10 2 30 40 10 00
11 165 11 2 45 41 10 15
12 180 12 2 00 42 10 30
13 195 13 3 15 43 10 45
14 210 14 3 30 44 11 00
15 225 15 3 45 45 11 15
16 240 16 4 00 46 11 30
17 255 17 4 15 47 11 45
18 270 18 4 30 48 12 00
19 285 19 4 45 49 12 15
20 300 20 5 00 50 12 30
21 315 21 5 15 51 12 45
22 330 22 5 30 52 13 00
23 345 23 5 45 53 13 15
24 360 24 6 00 54 13 30
25 6 15 55 13 45
26 6 30 56 14 00
27 6 45 57 14 15
28 7 00 58 14 30
29 7 15 59 14 45
30 7 30 60 15 00
Beispiel:
1 h 31 min entsprechen ... ?
(Ergebnis: 15 o plus 7 o 45´ = 22 o 45´)
Beispiel:
24 h 35 min 10 sec entsprechen ... ?
Nachschlagen in obiger Tabelle!
360o (für 24 h)
+ 7o 30´ (für 30 min)
+ 1o 15´ (für 5 min)
+ 2,5 ´´ (für 10 sec)
368o 45´ 02.5´´ =
- 360 ... ...
8o 45´ 02.5´´
Wichtig ist, dass man Grad, Minuten und Sekunden deutlich auseinander schreibt.
- - - - -
Am Ende des Nautischen Jahrbuchs gibt es eine ähnliche Tabelle (blaue Seiten), in der die Umrechnungen
für Sonne, Frühlingspunkt und Mond aufgelistet sind.
Sie heißt "Schalttafel".
Die Angaben im Bogenmaß nennen sich dort "Zuwachs Grt".
Es gibt verschiedene Möglichkeiten der Umrechnung von Zeit in Bogenmaß (und umgekehrt):
- Umrechnen wie oben vorgeführt
- Umrechnen mittels Rechner (dabei müssen einige Tasten gedrückt werden)
- Umwandeln mittels der obigen Tabelle oder der Tabelle im NJ.
Ich halte die Umwandlung mittels Tabelle als die am wenigsten fehleranfällige Methode.
- - - - -
Beispiel:
- 9 h 43 min 30 s. Umrechnen in Bogenmaß mit Tabelle:
9 h 135 o
43 min 10 o 45 ´
30 sec 7 ´ 30 ´´
145 o 52 ´ 30 ´´
Beispiel (Wikipedia):
Zum Beispiel bedeuten 1h 23m 45s (im Stundenmaß) und 20° 56' 15″ (im Gradmaß) dasselbe.
Wir wollen das überprüfen:
1 h entsprechen 15o
23 min entsprechen 5o 45´
45 sec entsprechen 11´ 15´´
20o 56´ 15´´
Beispiel:
An einem Ort mit der Länge 15o West kulminiert die Sonne um ... ?
Länge 15o W:
Ergebnis des Nachschlagens: ... ?
15o W entsprechen 1 h.
Kulminiert also die Sonne auf 15o W um 0100 UTC?
15o W ist ein Meridian etwas westlich von Irland.
Dort kann doch die Sonne nicht nachts um 0100 UTC (d. h. 1 h nach Mitternacht) kulminieren!
Wo liegt der Fehler?
Die Sonne kulminiert in Greenwich nicht um 00.00 UTC sondern um 12.00 UTC.
Zu 12.00 UTC muss die Stunde addiert werden.
Sie kulminiert also auf 15o W um 13.00 UTC.
Genaueres im folgenden Kapitel.
- - - - -
Bisher wurden nur W-Längen in Bogenmaß umgewandelt.
Das Bogenmaß reicht bis 360o. Aber W-Längen enden bei 180o W.
Verfahren bei E-Längen: später.
6. Mittagslänge, Mittagsposition
6.1 Mittagslänge
Länge des Sonnen-Bildpunktes als Zeit
Noch einmal:
Grundlage von Zeitmessungen ist die Sonne und deren Lauf um die Erde in 24 Stunden.
Der Bildpunkt der Sonne wandert in 1 h um 15o nach Westen, in 24 h um 360o.
Es gibt demnach einen unmittelbaren Zusammenhang zwischen der Position des Bildpunktes ("Länge") und der Zeit:
15o W entspricht 1 h,
30o W entsprechen 2 h, usw.
Deshalb kann man geographische Länge auch in Zeit ausdrücken.
Sowohl die geographische Koordinaten als auch die Koordinaten des Bildpunktes der Sonne werden vom Greenwicher Meridian aus gemessen.
Aber ...
Greenwicher Stundenwinkel (auch "Greenwichwinkel"; Grt, tGr; Greenwich Hour Angle, GHA )
Der Betrachter sieht auf den Nordpol. Die gelben Kreise symbolisieren die Sonne.
Der Greenwicher Stundenwinkel entspricht der Länge eines Gestirns, z. B. der Sonne
(genauer: der mit der Erddrehung wandernden Länge des Sonnenbildpunktes).
Knopp:
Der Greenwicher Stundenwinkel Grt ... eines Gestirns ist dessen Winkelabstand vom Meridian von Greenwich ...
Die Grt werden im Nautischen Jahrbuch für volle Stunden angegeben.
In Folge der Rotation der Erde ändern sie sich um etwa 15o pro Stunde.
Nautisches Jahrbuch:
Der Greenwischer Stundenwinkel ändert sich um ungefähr 1o in 4 Zeitminuten.
Deshalb muss seine Angabe in kurzen Zeitabständen erfolgen, um dazwischen liegende Werte ... berechnen zu können.
Greenwicher Stundenwinkel - Weltzeit
Vom Greenwicher Stundenwinkel (GHA / Grt) zu unterscheiden ist die Weltzeit (UTC).
Die Sonne kulminiert in Greenwich um 12.00 UTC. Der Stundenwinkel der Sonne (GHA/Grt) aber beträgt in diesem Moment 0o.
Eine Stunde später, also UTC 13.00, beträgt der Stundenwinkel der Sonne GHA/Grt 15o.
2 h später, also UTC 14.00, beträgt der Grt (GHA) der Sonne 30o.
usw.
90o (GHA/Grt) legt die Sonne in 6 h zurück. Also kulminiert sie dort (in 90o W) um (12.00 + 6.00 = ) 18.00 UTC.
Überall dort, wo die Sonne kulminiert ist "Schiffsmittag".
Das ist mit der lokalen Zeit einigermaßen übereinstimmend (s. Zonenzeit, Terrestrische Navigation), nicht aber mit UTC.
Diese verschiedenen "Uhren" muss man auseinanderhalten.
Messprobleme für den Navigator
Die Tagesbahn der Sonne ist für einen Beobachter ein auf- und absteigender Bogen am Himmel.
Der höchste Punkt dieses Tagbogens heißt "Kulmination".
In den auf- und absteigenden Bogenteilen verändert sich die Position der Sonne in ihrer Höhe rasch.
Aber die Sonne verweilt relativ lange im Scheitelpunkt (etwa 4 min), so dass zwar die Höhe gut gemessen,
nicht aber die Zeit sekundengenau festgestellt werden kann.
Deshalb wendet man einen Kniff an:
- Man hält die Zeit für eine Höhe im aufsteigenden Teil des Bogens fest.
- Wenn die absteigende Sonne diese gleiche Höhe wieder erreicht, notiert man die Zeit erneut.
Zeit der Kulmination ist dann die Mitte der beiden Zeiten (aus gleichen Höhen).
Uhr
Voraussetzung ist eine sekundengenau gehende Uhr.
Man erhält Zeitzeichen über bestimmte Kurzwellen-Sender, z. B. von
auf 2500 / 5000 / 10000 / 15000 / 20000 kHz.
Man muss die Uhr, nach der man rechnet, entsprechend stellen oder den etwaigen Fehler rechnerisch berücksichtigen.
- - - - -
Transit (Kulmination, T) vorherberechnen
Beispiel 1 (W)
Wann (in UT) kulminiert die Sonne in W 20 o 10 ` ?
- Rechnung:
Die Erde dreht sich um 360o in 24 h. Wie lange braucht sie für 1o ?
Den 360. Teil von 24 h.
24 h sind 24 x 60 min = 1440 min. Davon der 360. Teil: 1440 : 360 = 4 min
1o entsprechen 4 min
1´ ist der 60. Teil eines Grades; 4 min sind 4 x 60 sec = 240 s; davon der 60. Teil …
1 ` entsprechen 4 sec
(Vgl auch oben: 5. Umrechnung von Zeit in Länge / Bogenmaß in Zeit)
20o ergeben 20 x 4 min = 80 min (Zeitminuten) = 1 h 20 min
1´ ergeben 10 x 4 sec = 40 sec. 40 sec
1 h 20 min 40 sec
Um diesen Betrag kulminiert die Sonne gegen über Greenwich später. (also "plus")
Kulmination in Greenwich: 12 h 00 min UTC
+ 1 h 20 min 40 sec
13 h 20 min 40 sec UTC
In W 20 o 10 ` kulminiert die Sonne um "
- Schalttafel des NJ
Ausgehen in der Tabelle muss man vom Bogenmaß (o), und nicht von der Zeit (h, min).
Man muss also von rechts nach links lesen.
Der letzte angegebene Wert ist 14o 59,8´. Das reicht nicht.
Man muss also überlegen: Wie komme ich auf 20o ?
20o sind z. B. 2 x 10o
- Nachschlagen bei 10o ergibt 40 min + 0 s (sec).
2 x 40 min sind 80 min = 1h 20 min. 1h 20 min
- 10´ (Bogenmaß!) = 0o 10´.
Dortiger Wert: 40 s + 40 s
1h 20 min 40 sec
Um diesen Betrag ... s. oben.
Die Tücke der Tafeln besteht darin, dass man allzugerne Min (= Zeit) und ´ (= "Minuten" im Bogenmaß)
verwechselt.
Auch mit den Stellenwerten muss man aufpassen 10´ findet man bei 0o 10´.
- Zeitgleichung (= equation of time, e)
Leider wandert die Sonne nicht gleichmäßig.
Deshalb muss T (Transit, Kulmination) noch um die Zeitgleichung (= equation of time, e) korrigiert werden.
Im NJ als Tabelle: "Zeitgleichung, 12 Uhr UT".
Angenommen es handelt sich um den 15. Juli 2010
Für den 15. Juli 2010 wäre das z. B. - 5 min 59 s
13 h 19 min 100 s
- 5 59
13 h 14 min 41 s
Transit in 20o 10` W am 15. Juli 2010: 13 h 14 min 41 s
Die "Zeitgleichung" ist nicht konstant und muss für jedes Jahr neu berechnet werden.
-----------
Beispiel 2 (E)
Alles was östlich ist (östliche Längen), muss von UTC 12.00 h abgezogen werden.
Wann kulminiert die Sonne in 30 o E am 20. August 2010 ?
Rechnung:
30o entsprechen 30 x 4 min = 120 min = 2 h
12.00 h – 2 h = 10 h
10 00 00
Zeitgleichung (für 20. Aug. 2010) - 3 25
10 Uhr lässt sich schreiben als ...
09 59 60
- 3 25
09 56 35
Am 20. Aug. 2010 kulminiert in Sonne in 30 o E um 09 h 56 min 35 sec UTC
Nachschlagen:
30o sind 3 x 10o.
Wert für 10o = 40 min.
3 x 40 min = 120 min = 2 h
...
Praxis
In der Praxis genügt es, den Kulminationszeitpunkt einigermaßen zu schätzen und rechtzeitig mit den Messungen zu beginnen.
Mess-Vorgang
Entweder Transit (T, höchste Stelle der Kurve, Meridiandurchgang) vorherberechnen
oder ½ Stunde vor dem geschätzten T mit den Messungen beginnen.
- Alle 3 min Zeit und Höhen notieren.
- Nach dem Durchgang (wenn die Sonne den höchsten Punkt erreicht hat) Sextant auf eine geeignete Messung zurückstellen
- (den Wert dieser Messung am Sextant einstellen) und warten bzw. immer wieder durch den Sextant die Sonne betrachten.
- Wenn sich die Höhe wiederholt (der Unterrand der Sonne genau deckungsgleich mit dem Horizont ist), Zeit notieren.
- Die gemittelte Zeit der beiden Messungen (mit gleicher Höhe) ergibt die für die Längenberechnung wichtige Kulminationszeit.
- - - - -
Längenbestimmung
Zu Beispiel 1:
Datum: 15. Juni 2010
Angenommen man misst die aufsteigende Sonne um 13 h 12 min 20 sec
Und die absteigende Sonne mit der gleichen Höhe um 13 36 42
Man zählt zusammen und halbiert: 26 h 48 min 62 sec : 2 = 13 h 24 min 31 sec
Das ist der sekundengenaue Meridiandurchgang in UTC an der Schiffsposition.
Welcher geographischen Länge entspricht 13 h 24 min 31 sec UTC ?
Bei der Rückrechnung von der Zeit des Meridiandurchgangs (Transits, T) am Schiffsort zum Abstand Schiffsmeridian - Greenwichmeridian
gibt es (wie immer) zwei Wege:
- Umrechnung des zeitlichen Abstands in das Bogenmaß;
Dabei bedenken, ob die Kulmination vor oder nach der Kulmination in Greenwich erfolgt
und den errechneten Abstand nach W oder E abtragen. Zeitgleichung berücksichtigen.
- Den Abstand über den Stundenwinkel der Sonne (Grt im NJ, GHA) zu bestimmen.
Dann muss man im NJ nachschlagen, auf welcher Länge sich der Bildpunkt der Sonne
zum Zeitpunkt der Messung (= Schiffsposition) befindet.
Die den Tafeln unmittelbar entnommenen Zeiten und Winkel stimmen und brauchen nicht mit e korrigiert zu werden.
- Nachschlagen
Einfacher ist dieser Weg.
Wie groß ist der Grt/GHA der Sonne am 15. Juni 2010 zum Kulminations-Zeitpunkt 13 h 24 min 31 sec?
Nautisches Jahrbuch:
Di, 15. Juni, SONNE, UT1 13.00: Grt 014o 52,9 `
Schalttafel (blaue Seiten im NJ): 24 min, 31 s 6o 07,8 `
20o 60,7` = 21o 00,7 ` (Grt/GHA)
Umrechnung von 10tel - ´ (Min) in ´´ (Sek) :
(7 : 10) * 60 = 42 ´´
Schiffsposition: 21o 00,7 ` W bzw. 00´ 42 ´´ W
- Rechnen
Bei Rechnungen muss die Zeitgleichung (e) berücksichtigt werden: 15. Juni 2010, e = - 28 s
13 h 24 min 31 s UTC
e - 28
13 h 24 min 03 s
Kulmination (wahre Ortszeit, WOZ) um 13 h 24 min 03 s
Kulmination in Greenwich: 12 h 00 00
Zeitunterschied = Grt/GHA 1 h 24 min 03 s
Umrechnung Zeit in Länge (Bogenmaß)
zur Erinnerung:
1 h entspricht 15 o
1 min 15 ´
1 sec 15 ´´
Welcher Position entspricht ein Grt/GHA von 1 h 24 min 03 s ?
- 1h entsprechen 15o
- 1 min entsprechen 15 ´
24 min (24 x 15) entsprechen 360 ´ = 6o ... 06o
- 1 s entsprechen 15 ´´
3 s (3 x 15 = ) 45 ´´ ... - ´ 45 ´´
21o - ´´ 45 ´´ W
Schiffsposition: 21 o 00´ 45 ´´ W
(Der geringe Unterschied von 2´´ zum Ergebnis oben liegt an Auf- oder Abrundungen in den Tabellen.)
Deutlich geworden ist, um wie viel länger und fehleranfälliger das Rechnen ist.
- - - - -
Zur Veranschaulichung das ganze als Skizze.
Der Betrachter schwebt über dem Nordpol und sieht auf die Erde.
Formel für Mittagslänge West:
Mittagslänge W = GHA
Für die östlichen Längen muss umgedacht werden.
Der Greenwich-Stundenwinkel (Grt/GHA) wird nur nach W gemessen, von 0o bis 360o.
Die geographische Länge dagegen wird nur jeweils bis 180o gezählt; nach W bis 180o (W) und nach E bis 180o (E).
Formel für Mittagslänge Ost
Mittagslänge E = 360 - GHA
Noch einmal mit anderen Worten:
Bei Schiffsmittag befindet sich der Bildpunkt der Sonne auf demselben Meridian wie das Schiff, nämlich genau im Süden (oder N).
Daher
1) Westlänge = GHA (Bildpunktlänge bei Schiffsmittag)
2) Ostlänge = 360 o - GHA
- - - - -
Beispiel 3
Im Atlantik (W = westlich von Greenwich) am 15. Juni 2010 ; Kulmination 13 h 40 min
Länge?
Verfahren: Nachschlagen im NJ.
15. Juni 2010: 13 h GHA 14o 52,9 ´ 00 ´´
Schalttafel 40 min 10 00,0
GHA 24o 52,9 ´
Formel: Mittagslänge W = GHA
= 24 o 52,9 ` W
Beispiel 4
Im Mittelmeer (E, östl. von Greenwich), 15. Juni 2010; Transit 10 h 40 min UT
Länge?
GHA der Sonne (15. Juni 2010)
NJ UT 10 h 329o 53.3 `
Schalttafel 40 min 10 00.0`
GHA 339o 53.3`
Formel: Mittagslänge E = 360 o – GHA
= 360 o – 339o 53.3`
= 359o 60.0`
- 339 53.3`
20o 6,7` E
Länge = 20 o 06,7 E
- - - - -
6.2 Mittagsposition
Eine Position ergibt sich aus Breite und Länge.
Die Sextantmessung zur Kulmination ergibt die Breite (s. Mittagsbreite),
die halbierte Zeit aus der Summe der beiden Messungen mit gleicher Höhe ergibt die Länge (s. Mittagslänge).
Verfahren
Beim Messvorgang bestimmt man nicht nur die gleiche Höhe der auf- und absteigenden Sonne sondern auch den Kulminationspunkt.
Beispiel
Geschätzter Schiffsort: 145 W; 16. August 2010
Transit etwa: T Greenwich 12 h 00 min
+ 145o in Zeit = 145 x 4 min = 580 min = 9 h 40 min
21 h 40 min UTC
IE: - 0.4` Ah: 2 m; Sonnenunterrand
1. Messung: 21 h 20 min 30 s (UT),
2. Messung Sextablesung (Alt Sext): 45o 25,8` (Sonnunterrand)
3. Messung (gleiche Höhe wie 1.): 22 h 01 min 16 s
Breiten-Berechnung: Sext. 45o 25.8`
IB + 0.4
45 26.2
GB NJ + 12.6
Zusatzbeschickung für Aug. - 0.2
Wahre Höhe (True Alt) 45o 38.6`
Deklination der Sonne, 16. Aug. 2010, UT 12.00: 13o 14,6 N
Formeln:
LAT = ZD + Dec (+ wenn gleichnamig)
ZD = 90o - True Alt
ZD = 90o - 45 38.6
= 89 60
- 45 38.6
ZD = 44o 21.4`
LAT = ZD + Dec
LAT 44o 21.4
+ Dec 13o 14.6
Breite (LAT) 57 o 36.0` N
Längenberechnung
1. Messung 21 h 30 min 30 sec
3. Messung 22 01 16
43 31 46 : 2 =
21 h 30 min + 15 min, 30 s + 23 s
Transit, UT 21 h 45 min 53 s
Verfahren: Nachschlagen im NJ:
NJ: GHA (16. Aug. 2010) für 21 h 45 min 53 s
NJ 21 h 133o 56,6´
Schalttafel 45 min 53 s 11o 28,3
144 84.9 =
Grt/ GHA 145o 24.9´ W
Formel: Mittagslänge W = GHA
= 145 o 24.9 W
Das Schiff befindet sich auf 57 o 36.0` N und 145 o 24.9´ W.
- - - - -
Wer sich bis hierher durchgekämpft hat, sollte Routine durch Übung anstreben.
Ich empfehle, das aktuelle Nautische Jahrbuch zu erstehen und alle Beispiele mit den aktuellen Werten zu berechnen.
Dadurch dürften die Ergebnisse nicht weit auseinanderliegen.
Gleichzeitig hat man eine Kontrolle.
- - - - -
7. Standortbestimmung aus 2 Messungen
In der Praxis überlässt man die Auswertung der Sextantmessungen gerne einem Rechner.
Wenn man verstehen oder selbst rechnen will, muss man sich mit sphärischer Geometrie, nämlich dem Nautischen Dreieck beschäftigen.
Um zu rechnen, braucht man die entsprechenden mathematischen Kenntnisse.
Auch hier helfen Taschenrechner.
Den Wissenshintergrund liefert ein Lehrbuch.
Ich empfehle
Helmut Knopp, Astronomische Navigation, Verlag Busse Seewald
Knopp geht auch auf den Einsatz von Taschenrechnern ein.
Die entsprechenden Artikel im Internet zeigen die Zusammenhänge oft sehr anschaulich durch Skizzen oder Modelle.
Beispielsweise
http://wp.astrosail.com/tutorial/astronomische-navigation/koordinatensysteme/das-sphaerisch-astronomische-grunddreieck/
Spezielle Astro-Navigations-Rechner (z. B. Cassens&Plath: StarPilot TI-89 510,50 €; Mai 2019)
enthalten nicht nur das entsprechende Rechenprogramm sondern meist auch alle Angaben, die sonst das Nautische Jahrbuch liefert.
In der Regel arbeiten Astro-Rechner mit dem Höhendifferenzverfahren (nach Marcq Saint-Hilaire).Eine Gestirnsmessung, z. B. der Sonne, ergibt dabei letzten Endes eine Standlinie. Damit die nächste Standlinie in einem sinnvollen Winkel die erste Standlinie schneidet und sich dadurch ein realistischer Standort gewinnen lässt,
muss man wenigstens 4 Stunden bis zur nächsten Gestirnsmessung warten (Problem der "Schleifenden Schnitte").
Sehr viel weniger Zeit benötigt das Tagbogenverfahren.
Bereits nach zwei Stunden erhält man einen brauchbaren Standort. (s. dort)
Grundgedanke des Höhendifferenz-Verfahrens
Das Prinzip gilt für alle Gestirne. Ich beschränke mich auf die Sonne.
Angenommen man würde die Höhe einer Straßenlaterne mit dem Sextanten bestimmen. Der ermittelte Winkel sei 45o.
Wenn man die Richtung zum Laternenpfahl (in astronomischer Navigations-Sprache: zum "Bildpunkt" der Laterne) nicht kennt,
kann man über die eigene Position nur aussagen, dass sie sich irgendwo auf einer Kreislinie um die Laterne befindet,
deren Abstand mit dem gemessenen 45o - Winkel zusammenhängt.
Entsprechendes gilt für eine Sonnenmessung.
Zwei Sonnenmessungen in angemessenem zeitlichen Abstand ergeben zwei Kreise (von mehreren 1000 km), die sich in zwei Punkten schneiden.
Einer davon, nämlich der geographisch wahrscheinlichere, ist unser Standort.
Zeit
In den gesamten Überlegungen spielt die sekundengenaue Weltzeit UTC eine entscheidende Rolle.
Denn die Länge des Sonnenbildpunktes entspricht dem aktuellen zeitlichen Abstand des Bildpunktes vom Null-Meridian.
Deshalb wird die Länge des Sonnenbildpunktes "Greenwicher Stundenwinkel" (Grt; Engl.: Greenwich Hour Angel, GHA) genannt.
Gewöhnungsbedürftig ist, dass "Zeit" einen Abstand (Länge) beschreibt.
(Ausführlich dargestellt in: 4.5 Mittagslänge, Mittagsposition).
Der Abstand der Meridiane von Schiffsposition und Sonnenbildpunkt heißt
"Orts-Stundenwinkel" (Ort, Engl.: Local Hour Angle, LHA).
Wie man ihn erhält, zeigen Skizze und Beschreibung am Ende dieses Abschnittes.
Genau dieser Abstand ergibt die Standlinie.
Azimut – Richtung zur Sonne
Mit Hilfe der
- (gekoppelten) Breite des Beobachtungsortes,
- der Sonnenhöhe (Sextantmessung),
- der sekundengenauen Uhrzeit der Messung in UTC,
- dem im NJ nachzuschlagendem Bildpunkt (BP) der Sonne zur Messzeit
- und der sich daraus ergebenden Länge der Schiffsposition (Ortsstundenwinkel)
lässt sich mit Hilfe der mathematischen Zusammenhänge des Nautischen Dreiecks die Richtung zur Sonne (das Azimut) berechnen.
Die gekoppelte Schiffsposition liefert dabei den Punkt (Länge und Breite), von dem man aus die Richtung zum Sonnenbildpunkt
abtragen kann.
Das Azimut ist der Richtungsstrahl vom Beobachtungsort zum Sonnenbildpunkt.
Der Beobachtungsort liegt auf dem oben erwähnten Kreis um den BP der Sonne, dessen Durchmesser mehrere 1000 sm beträgt.
Auf einem kleinen Kartenausschnitt (unsere Seekarte) wird dieser Kreisausschnitt zu einer Geraden.
Es ist unsere Standlinie und verläuft im rechten Winkel zum Azimut.
Dabei gibt es zwei Probleme:
- das Problem der "schleifenden Schnitte". Man muss etwa 4 h bis zur 2. Messung warten.
- Während dieser Zeit macht aber die Yacht Strecke. Diese Distanz muss berücksichtigt werden:
die erste Standlinie muss "versegelt" werden.
Der Rechner erledigt nach Eingabe der notwendigen Werte die Rechenarbeit
und spuckt den Beobachtungsstandort zum Zeitpunkt der zweiten Messung aus.
- - - - -
HO - Tafeln, Höhendifferenzverfahren
Es gibt ein Verfahren, mit dem man, ohne zu rechnen, die eigene Position finden kann:
das Höhendifferenzverfahren in Kombination mit den HO –Tafeln (Sight Reduction Tables for Air Navigation, Pub No 249).
(Der "normale" Astro-Lehrgang arbeitet damit.)
In diesem Tafelwerk sind tabelliert:
- alle ganzgradigen Breiten von 0o bis 89o (aufgeteilt in 2 Bände),
- die Deklination der Sonne von 0o bis 29o,
- der LHA (Erläuterung später).
Das sind die Eingangswerte.
Man erhält:
- die zum "Rechenstandort" zugehörige (Sonnen-)Höhe,
- und das Azimut von dort aus.
Wenn der gemessene Sextantwinkel mit dem tabellierten Sextantwinkel der HO-Tafeln überstimmen würde,
wäre das Schiff genau auf der Standlinie (im rechten Winkel zum Azimut).
In der Regel ist das nicht der Fall, denn der Schiffsort wird kaum mit dem Koppelort übereinstimmen, geschweige denn ganzgradig sein.
Wenn sich aber der Winkel, den wir mit dem Sextanten gemessen haben, von jenem unterscheidet,
den die Tabelle zum Rechenort ausgibt, wo befindet sich dann tatsächlich unsere Standlinie?
Wir greifen noch einmal auf das eingangs erwähnte Beispiel mit der Laterne zurück:
Angenommen, der Winkel, unter dem wir die Laterne gemessen haben, betrug 45o 30`.
Ein (fiktives) Tafelwerk nennt zu unserem angenommenen Rechenort 46o.
Ist dann der Beobachter näher oder weiter entfernt vom Rechenort (und dem dazugehörigen Sextantwinkel)?
Näher ist man, wenn man mehr nach oben schauen muss, wenn also der Blickwinkel größer ist.
Wenn man weiter entfernt ist, wird der Beobachtungswinkel (= Sextantwinkel) kleiner.
45o 30` ist weniger als 46o. Also ist der Beobachter weiter entfernt (vom Laternen-Fußpunkt).
Das gleiche gilt von der Sonne.
Nun benötigt man ein Blatt Papier, am besten kariertes oder Millimeter-Papier.
Den Maßstab in nautischen Meilen legt man selbst fest, desgleichen die Einteilung in Breite und Länge.
- Man zeichnet die ganzgradig angenommene Position ein,
- anschließend von hier aus den Azimutstrahl
- und im rechten Winkel dazu die zum angenommenen Standort gehörige angenommene Standlinie (Gerade als Teil eines Kreises).
Einer Nebentabelle (der Tafeln) kann man die Strecke entnehmen, die der Differenz des gemessenen Sextantwinkels
zum tabellierten Sextantwinkel entspricht.
- Diese Strecke trägt man auf dem Azimutstrahl in Richtung Fußpunkt der Sonne ab, wenn der gemessene Sextantwinkel größer war.
War der gemessene Winkel kleiner, wird die Strecke in die Gegenrichtung abgetragen.
- Durch den Endpunkt der abgetragenen Strecke und parallel zur angenommenen ganzgradigen Standlinie
findet man die tatsächliche Standlinie, auf der sich unser Schiff befindet.
4 Stunden später misst man erneut die Sonne und bestimmt die dazugehörige Standlinie.
Der Schnittpunkt mit der versegelten ersten Standlinie ist die aktuelle Schiffsposition.
- - - - -
Praxis
Wie immer muss man den Fachwortschatz erlernen.
In diesem Fall handelt es sich um englische Begriffe.
Denn die HO-Tafeln wurden ursprünglich für die amerikanisch-englischen Bomberpiloten im 2. Weltkrieg entwickelt
und werden vom Verteidigungsministerium der Vereinigten Staaten herausgegeben.
Rechenschema
Fast überall werden schematisierte Rechengänge als Vordrucke zur Verfügung gestellt.
Sie sind sinnvoll, um gedankliche Fehler, die sich auf einem schwankenden Schiff gerne einstellen, zu minimieren.
Doch allein die Anwendung dieser Listen zu erlernen, ohne den Hintergrund zu verstehen,
ist für einen denkenden Navigator/Skipper unbefriedigend.
Nun müsste die praktische Arbeit mit den HO-Tafeln folgen
... (die ich hier nicht mehr darstelle.
Ich verweise auf diverse Anleitungen: in Büchern, im Internet; vielleicht kann man auch einen Lehrgang besuchen.)
Gegen die Anschaffung der HO-Tafeln wird eingewendet, man müsse 6 dicke Bücher kaufen.
Das ist nicht der Fall.
Zunächst: Es gibt zwei Tafel-Werke.
- Sight Reduction Tables for Air Navigation, Pub. Nr. 249
- Sight Reduction Tables for Marine Navigation, Pub No. 229
Letztere sind 6-bändig. Sie sind zwar genauer, aber deutlich umständlicher zu handhaben.
Sight Reduction Tables for Air Navigation, Pub No 249
Band I: Fixsterne; Breiten von 89o N bis 89o S
Diesen Band braucht man in der Regel nicht.
Band II: für die Breiten von 0o bis 39o
„... provide complete data for … sun, moon, planets, and stars within
the declination range of these bodies ...”
Band III: wie Bd II, aber für die Breiten 40o – 90o.
Die HO-Tafeln 249 sind auch im Internet verfügbar: https://thenauticalalmanac.com/Pub.%20No.%20249.html
Der 40. Breitengrad verläuft etwa zwischen Lissabon und Porto – Valencia – Mitte Sardinien – Otranto – Limnos (nördl. Ägäis).
Wer eine Weltumsegelung plant, braucht also die Bände II und III, dazu natürlich den aktuellen Nautischen Almanach.
Zum Üben genügt einer der Bände je nach eigenem Übungsort.
Ich verweise noch einmal auf
Helmut Knopp, Astronomische Navigation.
Präzise Erklärungen, verständliche Skizzen, Beispiele zum Üben.
Zum Schluss ein Satz von Mary Blewitt ("Praktisches Navigieren nach Gestirnen"):
„... und ich versichere jedem Anfänger, dass das Triumphgefühl die Mühe lohnt, wenn eine Standortbestimmung sich als richtig erweist.
Es ist nur der erste Schritt schwierig.
Nimm eine Höhe, und du wirst ein wenig verwirrt sein; nimm die zweite, und der Nebel wird sich lichten;
nimm ein Dutzend weitere, und du wirst nicht mehr verstehen, was für ein Theater vorher um das alles gemacht wurde.“
- - - - -
Begriffe
auch die Begriffserklärungen bei 4.2 "Nordsternbreite" und 4.4 "Mittagsbreite"
Stundenwinkel (Grt) eines Gestirns (Greenwich Hour Angle, GHA), z. B. der Sonne.
Es ist der Winkelabstand eines Gestirns (z. B. der Sonne) vom Meridian von Greenwich (0 - Meridian).
"Er entspricht der geographischen Länge eines Punktes der Erdoberfläche.
Ein Unterschied ist jedoch, dass der Grt immer in westlicher Richtung von 0 o bis 360 o gezählt wird." (Klopp)
Ortsstundenwinkel (t) - Local Hour Angle (LHA)
Nach Klopp:
Bezieht man den Stundenwinkel auf den Ortsmeridian eines Beobachters, nennt man ihn Ortsstundenwinkel (t)
(oder Local Hour Angle, LHA.)
Nach Plewitt: Auch (der) LHA wird in westlicher Richtung gemessen.
Nach Nautisches Jahrbuch:
Den Ortsstundenwinkel erhält man aus dem Greenwicher Stundenwinkel durch ...
Addition der geographischen Länge (östliche Länge positiv, westliche Länge negativ).
Erläuterung gibt die folgende Skizze:
Aus der Skizze ergibt sich:
- bei westlicher - Position des Schiffes:
Ortsstundenwinkel (t) = Greewichwinkel (Grt) minus Länge W (Lambda W)
t = Grt - Länge W
in E: LHA = GHA - Long W
- bei östlicher Position des Schiffes:
Ortsstundenwinkel (t) = Greenwichwinkel (Grt) plus Länge E (Lambda E)
t = Grt + Länge E
in E: LHA = GHA + Länge E
Merkhilfe:
Bei Westlänge: weniger
Die HO-Tafeln verlangen als Eingangswerte ganzzahlige Werte für den LHA.
- - - - -
Literatur
„Nautisches Jahrbuch – Ephemeriden und Tafeln“,
Bundesamt für Seeschifffahrt und Hydrographie, Hamburg
Knopp, Helmut, "Astronomische Navigation mit Tafeln, Taschenrechner und PC", Busse-Seewald, 1996
Internet: z. B. Wikipedia, aber auch andere Veröffentlichungen.
Dr. Hans Lampalzer
- - - - -
IV Tagbogen-Verfahren
Das Tagbogen-Verfahren ist nach der Sonnenbahn über dem Horizont, dem Tagbogen, benannt.
Es wurde von Dr. Ralf Lampalzer entwickelt
und 1988 in der "Deutschen Hydrographischen Zeitschrift" des "Deutschen Hydrographischen Instituts Hamburg" publiziert
(01/1988, Vol. 41, Ausgabe 1, S. 35 – 38)
unter dem Titel:
"Bestimmung der geographischen Position aufgrund mehrerer Messungen mit Fehlerrechnung"
Einführung von Dr. Ralf Lampalzer
Fast alle astronomischen Messungen werden heute nach dem Höhendifferenzverfahren ausgewertet.
Das Verfahren läuft darauf hinaus, mit Hilfe einer geschätzten Position eine astronomischen Messung in eine Standlinie
auf der Seekarte zu verwandeln.
Nach mehreren Messungen kann man dann mit Hilfe sich schneidender Standlinien eine Position ermitteln.
Mittlerweile erledigen oft Computer die lästige Auswertungsarbeit.
Diese Geräte sind klein, batteriebetrieben und damit für den Einsatz an Bord geeignet.
Intern im Rechner wird fast immer das Höhendifferenzverfahren als Grundlage des Rechnerprogramms verwendet.
Dabei sind astronomische Standlinien keine Bleistiftstriche, sondern Geradengleichungen.
Dennoch nützt das Höhendifferenzverfahren die Möglichkeiten des Computers in keiner Weise aus.
Auch ich wollte ursprünglich dieses Verfahren für den eigenen Gebrauch programmieren.
Dabei wurden mir jedoch verschiedene Nachteile des Höhendifferenzverfahrens bewusst:
- Das Verfahren orientiert sich an der Ebene der Seekarte und nicht an der Erde als Kugel.
Dadurch arbeitet das Verfahren nicht genau, besonders wenn die eigene Position schlecht geschätzt (gekoppelt) wurde.
- Normalerweise wird beim Höhendifferenzverfahren mit zwei Messungen gearbeitet.
Bei nur zwei Messungen können sich unvermeidliche Messfehler so fatal auswirken, dass der Standort sehr ungenau wird.
- Nur wenige Computerprogramme erlauben es, mehr als zwei Messungen einzugeben.
Gerade dies aber wäre der richtige Ansatz, um mit den Mitteln der Fehler- und Ausgleichsrechnung die Genauigkeit der Ergebnisse
beträchtlich zu verbessern, weil Messfehler des Navigators auf diese Weise kompensiert werden können.
So entwickelte ich ein vollständig neues Verfahren, das sich an den exakten Formeln der Kugelgeometrie und der Fehlerrechnung orientiert,
das Tagbogenverfahren.
Prinzip
Bei meinem Verfahren wird mit Hilfe mehrerer Messungen zunächst die Bahn, die ein Gestirn über dem Horizont zurücklegt, rekonstruiert.
Diese Bahn entspricht einer ganz bestimmten Beobachtungsposition auf der Erde: dem eigenen Standort.
Aus der Kurve des Gestirns wird nun auf diesen Standort zurückgerechnet.
Aufgrund dieses Prinzips habe ich das Verfahren als "Tagbogenverfahren" bezeichnet.
Programmierung, Rechner
Der nächste Schritt war die Erstellung eines Rechenprogrammes, das die Messungen auswertet.
Der Sharp PC 1403H erwies sich als geeignet.
Eingearbeitet wurden:
- Versegelung
Auf einem segelnden Schiff wird zwischen den Messungen eine Strecke zurückgelegt.
Dadurch ändern sich die Höhen geringfügig, aber doch so, dass man sie berücksichtigen sollte.
Das Programm bezieht die versegelte Strecke zwischen den Messungen mit ein, wenn der Benutzer eine entsprechende Einstellung vornimmt.
- Ausreißertest
Es kommt vor, dass sich ein grober Messfehler einschleicht. Dieser Messwert kann mit diesem Programmteil ausgesondert werden.
Der Rechner erkennt solche Ausreißer, sofern genügend Vergleichsmessungen vorliegen.
Dann zeigt der Rechner die Nummer(n) dieser Messung(en) und entfernt sie für die weitere Rechnung.
Die Praxis zeigt, dass mit der Elimination des ersten Ausreißers die Genauigkeit des Ergebnisses sprunghaft verbessert wird.
- Bildpunktkoordinaten
Die Bildpunktkoordinaten der Sonne, des Mondes des Frühlingspunktes und aller 80 im Nautischen Jahrbuch aufgeführten Fixsterne
sind im Programm enthalten. Dadurch entfällt für diese Himmelskörper das Blättern im Nautischen Jahrbuch.
In der Praxis wurde der Mond bislang etwas stiefmütterlich behandelt, da die Berechnung seiner Ephemeriden und der Parallaxe kompliziert ist.
Das Programm übernimmt diese Arbeit.
Aus einer Messung der Sonne und einer des Mondes (z. B. am Abend) lässt sich sofort eine genaue Position ermitteln.
Dasselbe gilt für die Fixsterne.
- Korrektur der gemessenen Höhe
Die Korrekturen in Bezug auf Refraktion, Augeshöhe, Radius der Sonne und Mond sowie Horizontalparallaxe werden automatisch vorgenommen.
Ein Indexfehler des Sextanten muss vor der Eingabe berichtigt werden.
bis hierher Dr. Ralf Lampalzer
- - - - -
Erprobung
Clark Stede und Michelle Poncini hatten den Tagbogen-Rechner auf ihrer Fahrt im Jahre 1990 durch die Nordwest-Passage an Bord.
Es war die erste Fahrt von Ost nach West, die einer deutschen Yacht gelang.
(Nachzulesen in "Packeis, Sturm und rote Segel", Edition Erdmann, 1991)
Im gleichen Jahr brach der zweite Golfkrieg aus.
Die Amerikaner verhinderten im Zuge der militärischen Operationen, dass das Global Positioning System (GPS),
welches vom US-Verteidigungsministerium entwickelt worden war, von anderen genutzt wurde;
d. h. sie schalteten es ab.
Clark Stede musste plötzlich mit dem Sextanten navigieren.
Dabei griff er auf den mit dem Tagbogenverfahren programmierten Rechner zurück.
Clark Stedes erstes Fax an Ralf Lampalzer nach Bezwingung der Nordwest-Passage:
"Der Rechner samt Tagbogen-Verfahren ist ERSTE Klasse."
Rückblickend im o. g. Buch heißt es sachlich:
"Wir hatten zu Testzwecken von Herrn Ralf Lampalzer einen kleinen Sharp-Rechner an Bord, mit dem Programm Tagbogenverfahren.
Ohne einen Koppelort eingeben zu müssen, konnten wir mit den Eingaben
Gestirn, Datum, Uhrzeit, gemessene Höhe, Kurs und gesegelte Strecke
sehr genaue Positionsangaben erhalten."
Versuche, das Tagbogenverfahren bekannt zu machen
Im Anschluss daran versuchten wir, Bobby Schenk das Verfahren vorzustellen.
Immerhin war es das erste Verfahren, das anders dachte als Marcq St. Hilaire`s "Höhendifferenzverfahren" (entwickelt etwa 1875).
Naiv wie wir waren, glaubten wir, Bobby Schenk würde vielleicht die Rolle eines Mentors übernehmen
und - als damaliger Astro-Papst - diesem revolutionären Verfahren zum Durchbruch verhelfen.
Wir erträumten uns eine Art Zusammenarbeit.
Bobby Schenk hat zwar auf unseren ersten Kontakt geantwortet, dann aber nicht mehr.
Er hat uns wohl vor allem als Konkurrenten zu seinem Astro-Computer gesehen.
Nun versuchten wir es allein, und zwar mit Annoncen in Trans-Ocean und allen gängigen Segler-Zeitschriften.
Einer der wenigen, die sich daraufhin mit unserem Rechner ausrüsteten, war Helmut van Straelen.
("Beidrehen? … Im Orkan?", auf dieser Webseite)
Die YACHT verweigerte die Veröffentlichung unserer Anzeige mit der Begründung, es würde gegen ihre finanziellen Interessen verstoßen.
Erst jetzt realisierten wir, dass YACHT und Bobby Schenk zusammenarbeiteten und dass "finanzielle Interessen" dominierten.
Zum Schluss versuchten wir mit Clark Stedes Hilfe, einen anderen Partner zu finden.
Ein bekannter Segler, der Astro-Navigationskurse hielt, wollte unseren Rechner mit dem Tagbogenverfahren in seinen Kursen vorstellen.
Allerdings bestand er darauf, dass der Rechner mit dem Tagbogen-Programm seinen (!) Namen erhalten sollte.
Damit waren wir nicht einverstanden. Er gab sich zum Schein zufrieden, unterlief aber die vereinbarte Kooperation.
Nach zwei Jahren erfolgloser Anstrengungen gaben wir auf.
Gelernt hatten wir, wie gnadenlos die moderne Wirtschaftswelt ist.
Mittlerweile sind 30 Jahre vergangen.
Die Rechen-Computer haben sich verändert, ebenfalls die Programmiertechnik.
Wenn man das rechnerbasierte Tagbogen-Verfahren verfügbar machen wollte, müsste es mit den aktuellen Techniken
neu programmiert werden.
Dr. Hans Lampalzer, Mai 2019
Neuprogrammierung
Am 6. 6. 2022 erhielt ich eine Email:
...mit Interesse lese ich Ihren Netzbeitrag "Segeln" und bin dabei ... auf die Arbeit Ihres Sohnes bzgl. Tagbogverfahren gestoßen.
Ich beschäftige mich seit längerer Zeit damit, die historischen - mathematischen - Verfahren der astronomischen Navigation
zu verstehen (Borda 1771, Lalande 1793, Gauss-Methode) ...
Aus diesem Grunde möchte ich ... anfragen, ob Sie noch eine ... Kopie des entsprechenden Artikels
aus der Deutschen Hydrografischen Zeitschrift besitzen und mir diese zur Verfügung stellen könnten ... .
Mit freundlichen Grüßen
Dr. Ulrich Barkow
Am 8. 6. 2022 schrieb Dr. Barkow:
... das BSH hat mir mittlerweile freundlicherweise Fotokopien überlassen. ...
Helmut Hoffrichter hat auf seiner Seite SY-Zephir verschiedene Verfahren zur Positionsbestimmung als Excel Tabelle
zur Verfügung gestellt, am interessantesten jene basierend auf dem Verfahren von Gauß als auch das von Herrn Borda.
... Das Verfahren Ihres Sohnes geht da noch deutlich mathematischer weiter durch Fehlerbetrachtung multipler Messungen. ...
Es wäre zu schade, wenn ein solches Verfahren in Vergessenheit fiele.
25. 4. 2023
... anbei die aktuellste Version, hoffentlich weitgehend fehlerfrei. ...
Die Tabellen verzichten bewusst auf Makros / VBA, damit ist gewährleistet, dass diese auch auf Android oder Ipad mit EXCEL-App
lauffähig sind (praktisch für die Arbeit an Bord). ...
Wir stellen das Tagbogenverfahren in der neu programmierten Version von Herrn Dr. Ulrich Barkow,
mit seiner und Herrn Hoffrichters Einverständnis, kostenlos zum Download zur Verfügung.
Ein zweites Programm ist enthalten, die Positionsbestimmung nach Gauß, programmiert von Helmut Hoffrichter.
oder über
- - - - -
Aus dem damaligen Handbuch zum Rechnerprogramm:
Grundsätzliches zur astronomischen Navigation (von Dr. Ralf Lampalzer)
Die Messung einer Gestirnshöhe liefert keine Position.
Sie reduziert nur die möglichen Positionen des Schiffes auf alle Punkte eines Kreises, der sich über den ganzen Globus erstreckt.
Auf Ihrer Seekarte sehen Sie in aller Regel nur einen winzigen Teil dieses Kreises, der dann kaum noch eine Krümmung aufweist
und dem Navigator deshalb wie eine Gerade, wie die "Standlinie" vorkommt.
Eine Position kann grundsätzlich erst nach mindestens zwei Messungen ermittelt werden, weil sich dann die Kreise schneiden
– hoffentlich genau dort, wo sich das Schiff befindet.
Allerdings ist mit zwei Messungen desselben Himmelskörpers hintereinander noch nicht viel erreicht.
Die erhaltenen Kreise werden sich kaum unterscheiden, so dass die Standlinie über weite Strecken sehr eng beisammen liegen.
Es ergibt sich zwar rechnerisch ein Schnittpunkt, als exakter Standort ist er aber unbrauchbar.
Dieses Problem wird allgemein als Problem der schleifenden Schnitte bezeichnet.
Es wird üblicherweise dadurch vermieden,
- dass man in der Dämmerung verschiedene Himmelsobjekte misst:
die entsprechenden Kreise sind dann deutlich getrennt und schneiden sich sauber
- oder dass zwischen den Messungen ein und desselben Objektes ein ausreichend langer zeitlicher Abstand eingehalten wird.
Das Höhendifferenzverfahren wurde ca. 1875 von dem französischen Admiral Marcq St. Hilaire entwickelt.
Es liefert zu jeder Sextantmessung eine Standlinie. Da diese Standlinie Teil eines Kreises ist, benötigt das Höhendifferenzverfahren eine Angabe,
welcher Teil des Kreises in die Standlinie umgewandelt werden soll.
Deswegen ist für das Höhendifferenzverfahren eine ungefähre Angabe der Position nötig, z. B. der Koppelort eines Schiffes.
Je ungenauer diese Angabe, desto ungenauer arbeitet auch das Verfahren. ...
Das Tagbogenverfahren verwandelt Kreise nicht in Linien, sondern rechnet in den exakten Formeln der Kugelgeometrie.
Zusätzlich werden statistische Methoden einbezogen. …
Das Mittagsbesteck ist das älteste Verfahren der astronomischen Navigation.
Das besondere an diesem Verfahren ist, dass die Bestimmung der Breite und Länge unabhängig voneinander vorgenommen werden kann:
- die Breite aus der Kulminationshöhe ("Mittagsbreite", diese beherrschten schon die Phönizier)
- und die Länge aus der Kulminationszeit ("Mittagslänge", seit J. Harrisons Chronometer im Jahre 1759 möglich).
Im Tagbogenverfahren wird das Mittagsbesteck (Mittagsbreite und –länge) zu einem Spezialfall:
Es wird genau jener Teil des Tagbogens ausgemessen, in dem die Sonne kulminiert.
Also ist für die Mittagsbreite kein eigenständiges Programm nötig.
Für den Navigator ergibt sich der Vorteil, dass er nicht an bestimmte Messzeitpunkte gebunden ist, dass also der Zeitdruck entfällt.
Denn er braucht weder die Sonne exakt bei der Kulmination zu messen,
noch muss er den genauen Durchgang der absteigenden Sonne durch die anfangs gemessene Höhe treffen.
Und dennoch erhält er einen Standort mit gleicher Genauigkeit.
Statistische Betrachtungen
In der Praxis ist es fast immer so, dass tagsüber in möglichst kurzer Zeit ein Standort ermittelt werden soll.
Dies ist jedoch aufgrund des "Problems der schleifenden Schnitte" nicht mit einer brauchbaren Genauigkeit durchführbar.
Setzt man den Fehler bei einer Messzeit von 4 Stunden willkürlich gleich 1, so beschreibt folgende Tabelle
die Erhöhung des Fehlers durch schleifende Schnitte bei kürzeren Beobachtungszeiträumen:
Gesamtzeit 4 h 3 h 2 h 1 h 45 min 40 min 30 min
Fehler 1 1,2 1,7 3,3 4,4 5,0 6,6
(Diese Fehler rühren daher, dass der Schnittpunkt zweier nicht scharf bekannter Geraden, sich unter einem spitzen Winkel schneiden,
weniger genau bestimmt werden kann als wenn sie sich rechtwinklig schneiden.
Der Fehler ist proportional zur Fläche der Fehlerellipse zweier sich schneidender Geraden.)
Man kann diesen Fehler dadurch kompensieren, dass der Himmelskörper mehr als zweimal gemessen wird.
Der Rechner kennt dann eine Vielzahl von Kreisen, die er mit statistischen Methoden wesentlich genauer auswerten kann. ...
Vorgehen in der Praxis
Bewährt hat sich folgendes Vorgehen:
- Innerhalb einer Viertelstunde wird die Sonne mehrfach gemessen, vielleicht 5 mal, (auch 4 x dürfte ausreichend sein)
- dann wartet man eine Viertelstunde
- und misst anschließend innerhalb der dritten Viertelstunde erneut 5 mal.
Das reicht für eine seriöse Standortbestimmung mit Hilfe des Tagbogenverfahrens aus.
"Das Verfahren ermöglicht bei den typischen Messfehlern (Sextant freihändig gehalten, Seegang) von ca. 2'
eine für praktische Zwecke brauchbare Standortbestimmung in etwa 45 Minuten mit 10 Messungen." (Dr. Ralf Lampalzer)
Die größte Genauigkeit (bzw. den kürzesten Messzeitraum) erhält man um die Mittagszeit (Kulmination).
Es bleibt jedoch festzuhalten, dass andere Fehlerquellen auch starken Einfluss auf das Ergebnis haben:
- Messtechnik des Beobachters
- Eine präzise Uhr ist Voraussetzung.
Jede Sekunde, die die Uhr vor- oder nachgeht, verändert die berechnete Position um ¼` (~ 460 m) nach Westen bzw. Osten.
- Bei Verwendung eines Kunststoffsextanten muss der Fehler aus den obigen Tabellen höher angesetzt,
vielleicht verdoppelt werden.
Das heißt für die Praxis: öfter messen oder Messzeitspanne verlängern.
Vorteile des Tagbogenverfahrens
- Die Eingabe eines Koppelortes entfällt.
- Der Standort wird mit erhöhter Genauigkeit ermittelt.
- Eine Standortbestimmung ist nach kürzerer Zeit möglich.
- Der Zeitdruck entfällt, weil es nicht notwendig ist, bei der Messung bestimmte Zeitpunkte exakt einzuhalten (Mittagsbesteck).
Dr. Ralf Lampalzer (1990)
Den mathematischen Hintergrund hat Herr Helmut Hoffrichter in einer auch für Laien verständlichen Form dargelegt:
Nov. 2024





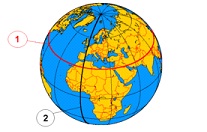
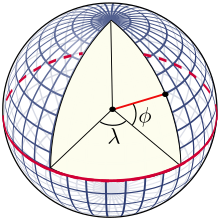
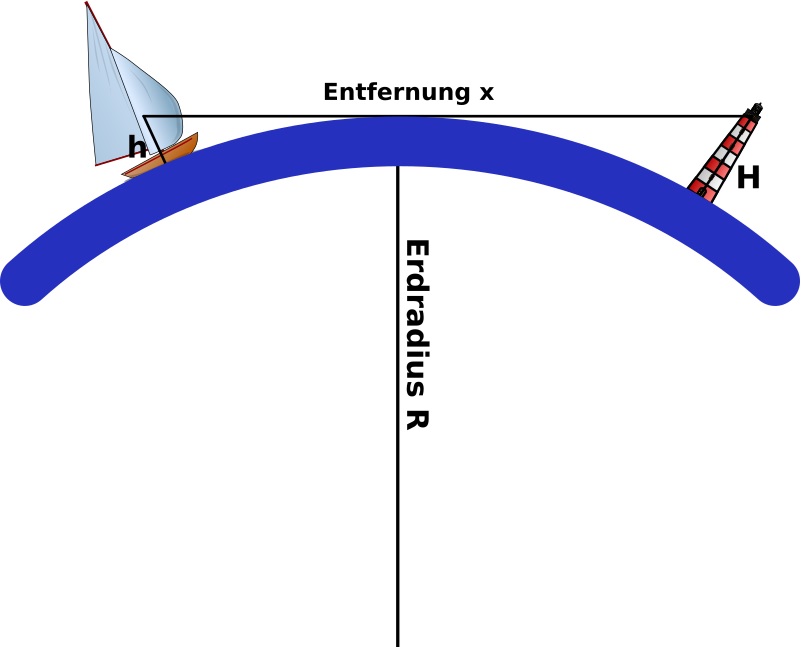
 (Wikipedia)
(Wikipedia)